题目内容
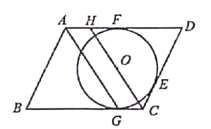
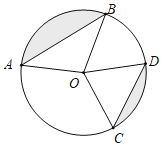
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,FD切
,FD切![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
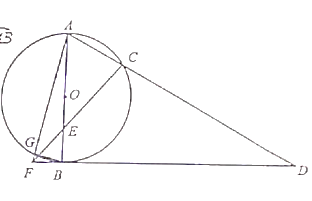
(1)求证:![]() ;
;
(2)若![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用圆周角定理及![]() ,求得∠ABC=30°,利用切线的性质求得∠D=30°,根据直角三角形30度角的性质从而证出
,求得∠ABC=30°,利用切线的性质求得∠D=30°,根据直角三角形30度角的性质从而证出![]() ;
;
(2)先证得△OAC为等边三角形,求得![]() 的长,过点C作CM⊥AO于点M,证出△CME∽△FBE,求出
的长,过点C作CM⊥AO于点M,证出△CME∽△FBE,求出![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,利用面积法即可求出
,利用面积法即可求出![]() .
.
(1) 连接BC,

∵AB是⊙O的直径,![]() ,
,
∴∠ACB=90°,∠ABC=30°,∠BAC=60°,
∴![]() ,
,
∵BD切![]() 于点
于点![]() ,
,
∴AB⊥DB,
∴∠D=90![]() ∠BAD=90
∠BAD=90![]() 60°=30°,
60°=30°,
∴AD=2AB,
∴AD=4AC,
∴![]() ;
;
(2) 连接OC,过点C作CM⊥AO于点M,

∵∠BAC=60°,OA=OC,
∴△OAC为等边三角形,
∴AC=OA=OC=2,OM=MA=1,
∵CM⊥AO,
∴OM=MA=![]() =1,
=1,
在![]() 中,
中, ![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∵BF切![]() 于点
于点![]() ,
,
∴AB⊥FB,
∴∠FBE=90![]() ,
,
∵∠FEB=∠CEM,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴ ,
,
∵AB是⊙O的直径
∴∠AGB=90°,
∴BG⊥AF,
∵![]() ,
,
∴![]() ,
,
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】名闻遐迩的秦顺明前茶,成本每斤500元,某茶场今年春天试营销,每周的销售量y(斤)与销售单价x(元/斤)满足的关系如下表:
x(元/斤) | 550 | 600 | 650 | 680 | 700 |
y(斤) | 450 | 400 | 350 | 320 | 300 |
(1)请根据表中的数据猜想并写出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利w元,试写w与x之间的函数关系式,并求出茶场每周的最大利润.
(3)若该茶场每周获利不少于40000元,试确定销售单价x的取值范围.