题目内容
【题目】已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
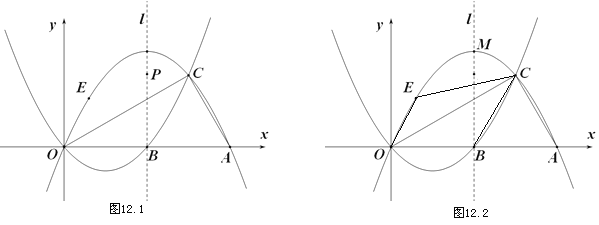
轴的一个交点坐标为![]() ,其部分图象如图所示,有下列结论:①
,其部分图象如图所示,有下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 增大而增大;④抛物线的顶点坐标为
增大而增大;④抛物线的顶点坐标为![]() ;⑤若方程
;⑤若方程![]() 两根为
两根为![]() (
(![]() ),则
),则![]() ,
,![]() .其中正确结论有( )
.其中正确结论有( )

A.1个B.2个C.3个D.4个
【答案】B
【解析】
由抛物线的对称轴结合抛物线与x轴的一个交点坐标,可求出另一交点坐标,结论①错误;当x=-1时,y>0,得到a-b+c>0,结论②错误;根据抛物线的对称性得到结论③错误;将x=2代入二次函数解析式中结合4a+b+c=0,即可求出抛物线的顶点坐标,结论④正确;根据抛物线![]() 的图象与直线
的图象与直线![]() 的交点情况判断⑤.
的交点情况判断⑤.
①∵抛物线![]() a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
∴抛物线与x轴的另一交点坐标为(0,0),
∴抛物线过原点,
∴![]() ,
,
∴![]() ,结论①错误;
,结论①错误;
②∵当x=-1时,y>0,
∴a-b+c>0,结论②错误;
③∵抛物线开口向上,
∴当x<2时,y随x增大而减小,③错误;
④抛物线![]() a≠0)的对称轴为直线x=2,且抛物线过原点,
a≠0)的对称轴为直线x=2,且抛物线过原点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴抛物线的顶点坐标为![]() ,结论④正确;
,结论④正确;
⑤∵抛物线与x轴的交点坐标为(4,0),(0,0),
∴抛物线的解析式也可以写作:![]() ,
,
方程![]() 两根
两根![]() ,可以看作是:抛物线
,可以看作是:抛物线![]() 与直线
与直线![]() 的两个交点的横坐标,
的两个交点的横坐标,
∴![]() ,结论⑤正确;
,结论⑤正确;
综上所述,正确的结论有:④⑤.
故选:B.

【题目】某商店销售一种商品,经市场调查发现,该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数.其售价、周销售量、周销售利润
(元/件)的一次函数.其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)求![]() 关于
关于![]() 的函数解析式(不写出自变量的取值范围);
的函数解析式(不写出自变量的取值范围);
(2)该商品进价是 元/件;求售价是多少元/件时,周销售利润最大,最大利润是多少元?
(3)由于某种原因,该商品进价提高了![]() 元/件(
元/件(![]() ),物价部门规定该商品售价不得超过65元/件.该商店在今后的销售中,周销售量与售价仍然满足(1)中函数关系.若周销售最大利润是1400元,则
),物价部门规定该商品售价不得超过65元/件.该商店在今后的销售中,周销售量与售价仍然满足(1)中函数关系.若周销售最大利润是1400元,则![]() 的值为 .
的值为 .