题目内容
 正方形ABCD的边长是4,将此正方形置于平面直角坐标系中,使AB落在x轴的正半轴上,C、D落在第一象限,经过点C的直线y=
正方形ABCD的边长是4,将此正方形置于平面直角坐标系中,使AB落在x轴的正半轴上,C、D落在第一象限,经过点C的直线y=| 4 |
| 3 |
| 8 |
| 3 |
(1)求四边形AECD的面积;
(2)在坐标平面内,求出经过点E且将正方形ABCD分成面积相等的两部分的直线.
分析:(1)求得C的坐标,以及E的坐标,则求得AE的长,根据直角梯形的面积公式即可求得四边形的面积;
(2)经过点E且将正方形ABCD分成面积相等的两部分的直线与CD的交点F到C的距离一定等于AE,则F的坐标可以求得,利用待定系数法即可求得直线EF的解析式.
(2)经过点E且将正方形ABCD分成面积相等的两部分的直线与CD的交点F到C的距离一定等于AE,则F的坐标可以求得,利用待定系数法即可求得直线EF的解析式.
解答:解:(1)在y=
x-
中,
令y=4,即
x-
=4,
解得:x=5,则B的坐标是(5,0);
令y=0,即
x-
=0,
解得:x=2,则E的坐标是(2,0).
则OB=5,OE=2,BE=OB-OA=5-2=3,
∴AE=AB-BE=4-3=1,
边形AECD=
(AE+CD)•AD=
(4+1)×4=10;
(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).
设直线的解析式是y=kx+b,则
,
解得:
.
则直线的解析式是:y=2x-4.
| 4 |
| 3 |
| 8 |
| 3 |
令y=4,即
| 4 |
| 3 |
| 8 |
| 3 |
解得:x=5,则B的坐标是(5,0);
令y=0,即
| 4 |
| 3 |
| 8 |
| 3 |
解得:x=2,则E的坐标是(2,0).
则OB=5,OE=2,BE=OB-OA=5-2=3,
∴AE=AB-BE=4-3=1,
边形AECD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).
设直线的解析式是y=kx+b,则
|
解得:
|
则直线的解析式是:y=2x-4.
点评:本题考查了正方形的性质与直角梯形的面积,待定系数法求函数解析式的综合应用,正确理解正方形的性质是关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 附加题
附加题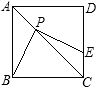 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3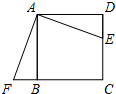 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=