题目内容
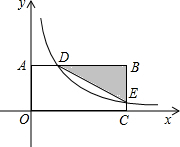 如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=
如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=| k |
| x |
| A、9.6 | B、12 |
| C、14.4 | D、16 |
考点:反比例函数系数k的几何意义
专题:
分析:首先设B(4a,b),E(4a,d),利用AD:BD=1:3,则D(a,b),进而利用△BDE的面积为18得出ab-ad=12,结合反比例函数图象上的性质得出ab=4ad,进而得出ad的值,即可得出答案.
解答: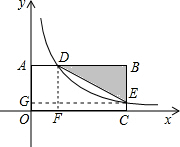 解:如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.
解:如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.
设B(4a,b),E(4a,d).
∵AD:BD=1:3,
∴D(a,b).
又∵△BDE的面积为18,
∴BD=3a,BE=b-d,
∴
×3a(b-d)=18,
∴a(b-d)=12,即ab-ad=12,
∵D,E都在反比例函数图象上,
∴ab=4ad,
∴4ad-ad=12,
解得:ad=4,
∴k=4ad=16.
故选:D.
 解:如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.
解:如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.设B(4a,b),E(4a,d).
∵AD:BD=1:3,
∴D(a,b).
又∵△BDE的面积为18,
∴BD=3a,BE=b-d,
∴
| 1 |
| 2 |
∴a(b-d)=12,即ab-ad=12,
∵D,E都在反比例函数图象上,
∴ab=4ad,
∴4ad-ad=12,
解得:ad=4,
∴k=4ad=16.
故选:D.
点评:此题主要考查了反比例函数综合应用以及三角形面积求法等知识,根据已知得出ab=4ad是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
计算(-
a2b)3的结果是( )
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
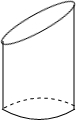 画出如图所示的立体图形的三视图.
画出如图所示的立体图形的三视图.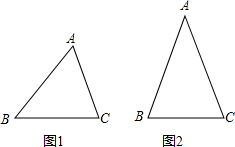 小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:
小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论: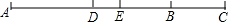 如图,已知A、B、C三点在同一直线上,AB=24cm,BC=
如图,已知A、B、C三点在同一直线上,AB=24cm,BC=