题目内容
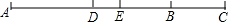 如图,已知A、B、C三点在同一直线上,AB=24cm,BC=
如图,已知A、B、C三点在同一直线上,AB=24cm,BC=| 3 |
| 8 |
考点:两点间的距离
专题:计算题
分析:先由BC=
AB得到BC=9,则AC=33,再根据线段中点的定义得到AE=
,AD=12,然后计算AE-AD即可.
| 3 |
| 8 |
| 33 |
| 2 |
解答:解:∵AB=24cm,BC=
AB,
∴BC=9,
∴AC=AB+BC=33,
∵E是AC的中点,D是AB的中点,
∴AE=
AC=
,AD=
AB=12,
∴DE=AE-AD=
.
| 3 |
| 8 |
∴BC=9,
∴AC=AB+BC=33,
∵E是AC的中点,D是AB的中点,
∴AE=
| 1 |
| 2 |
| 33 |
| 2 |
| 1 |
| 2 |
∴DE=AE-AD=
| 9 |
| 2 |
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
观察图中的图形,是中心对称图形的有( ) 

| A、2个 | B、1个 | C、4个 | D、3个 |
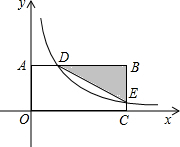 如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=
如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=| k |
| x |
| A、9.6 | B、12 |
| C、14.4 | D、16 |
 下图哪一个是正方体的展开图( )
下图哪一个是正方体的展开图( )A、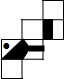 |
B、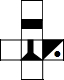 |
C、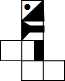 |
D、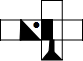 |
 如图,东西方向的海岸线上有A、B两个观测站,在A地发现它的北偏东60°方向有一条渔船C,同一时刻,在B地发现该渔船C在它的北偏西30°方向,试画图说明这条渔船的位置,并量出渔船C关于A、B两地视角(即∠ACB)的大小.
如图,东西方向的海岸线上有A、B两个观测站,在A地发现它的北偏东60°方向有一条渔船C,同一时刻,在B地发现该渔船C在它的北偏西30°方向,试画图说明这条渔船的位置,并量出渔船C关于A、B两地视角(即∠ACB)的大小.