题目内容
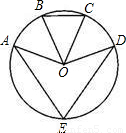（2012•青海）如图，已知点E是圆O上的点，B、C分别是劣弧AD的三等分点，∠BOC=46°，则∠AED的度数为 度．
【答案】分析：欲求∠AED，又已知B、C分别是劣弧AD的三等分点，∠BOC=46°，可求∠AOD=138°，再利用圆周角与圆心角的关系求解．
解答：解：∵B、C分别是劣弧AD的三等分点，∠BOC=46°，
∴∠AOD=138°，
∴∠AED=138°÷2=69°．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
解答：解：∵B、C分别是劣弧AD的三等分点，∠BOC=46°，
∴∠AOD=138°，
∴∠AED=138°÷2=69°．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
（2012•青海）如图反映的过程是：小刚从家去菜地浇水，又去青稞地除草，然后回家，如果菜地和青稞地的距离为a千米，小刚在青稞地除草比在菜地浇水多用了b分钟，则a，b的值分别为（ ）
（2012•青海）如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tanB的值是（ ）
（2012•青海）如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2m，BC=14cm，则楼高CD为
（2012•青海）如图，一次函数y=kx-3的图象与反比例函数y=
（2012•青海）如图，AB是⊙O的直径，弦CD⊥AB于点N，点M在⊙O上，∠1=∠C