题目内容
【题目】如图,在平面直角坐标系中,直线AB与函数y= ![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= ![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.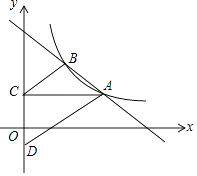
(1)求m,k,n的值;
(2)求△ABC的面积.
【答案】
(1)解:∵点A的坐标为(m,2),AC平行于x轴,
∴OC=2,AC⊥y轴,
∵OD= ![]() OC,
OC,
∴OD=1,
∴CD=3,
∵△ACD的面积为6,
∴ ![]() CDAC=6,
CDAC=6,
∴AC=4,即m=4,
则点A的坐标为(4,2),将其代入y= ![]() 可得k=8,
可得k=8,
∵点B(2,n)在y= ![]() 的图象上,
的图象上,
∴n=4;
(2)解:如图,过点B作BE⊥AC于点E,则BE=2,
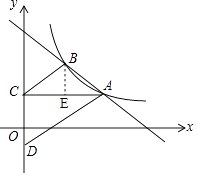
∴S△ABC= ![]() ACBE=
ACBE= ![]() ×4×2=4,
×4×2=4,
即△ABC的面积为4.
【解析】由AC平行,可得A、C的纵坐标相等,等于2,再由OD= ![]() OC,可得CD=3,由面积可求得AC=4,即m=4,进而求得n=4,k=8;(2)△ABC是水平三角形,可选择水平边AC作为底边,需过B作出AC边上的高,求出高即可求出面积.
OC,可得CD=3,由面积可求得AC=4,即m=4,进而求得n=4,k=8;(2)△ABC是水平三角形,可选择水平边AC作为底边,需过B作出AC边上的高,求出高即可求出面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目