Question

【题目】求证：两边分别相等且其中一组等边的对角相等的两个锐角三角形全等．

Answer 1

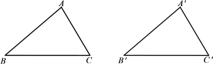
【答案】答案见解析

【解析】

画出图形，结合图形写出已知、求证，然后证明即可．

过点A作AD⊥BC于点D，过点A′ 作A′D′⊥B′C′于点D′，先证明△ACD≌△A′C′D′，得到AD= A′D′．再证明Rt△ABD≌Rt△A' B' D'，得到∠B =∠B'．最后证明△ABC≌△A' B' C'即可．

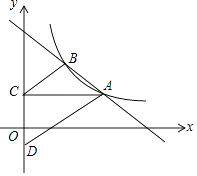
已知：如图，在锐角三角形ABC和锐角三角形△A′B′C′中，AB=A′B′，AC= A′C′，∠C=∠C′．

求证：△ABC≌△A′B′C′．

证明：过点A作AD⊥BC于点D，过点A′ 作A′D′⊥B′C′于点D′，∴∠ADC=∠A′D′C′=∠ADB=∠A′D′B′=90°．

在△ACD和△A′C′D′中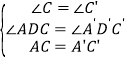，∵，∴△ACD≌△A′C′D′（AAS），∴AD= A′D′．

在△ABD和Rt△A′B′D′中，∵，∴Rt≌Rt（HL），∴∠ ∠．

在△ABC和△A' B' C' 中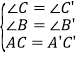，∵，∴≌（AAS）．