题目内容
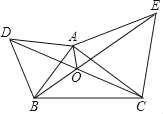
【题目】如图,△ABE为等腰直角三角形,∠ABE=90°,BC=BD,∠FAD=30°.

(1)求证:△ABC≌△EBD;
(2)求∠AFE的度数.
【答案】(1)见解析;(2)90°
【解析】
试题分析:(1)根据等腰直角三角形的性质得到AB=BE,根据邻补角的定义得到∠ABE=∠DBE=90°,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到∠BAC=∠BED,根据三角形的内角和得到∠BED+∠D=90°,等量代换得到∠BAC+∠D=90°,即可得到结论.
(1)证明:∵△ABE为等腰直角三角形,
∴AB=BE,
∵∠ABE=90°,
∴∠ABE=∠DBE=90°,
在△ABC与△BDE中,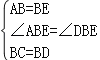 ,
,
∴△ABC≌△EBD;
(2)解:∵△ABC≌△EBD,
∴∠BAC=∠BED,
∵∠BED+∠D=90°,
∴∠BAC+∠D=90°,
∴∠AFD=90°,
∴∠AFE=90°.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目