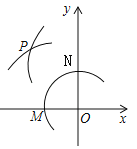��Ŀ����
����Ŀ��ij�����ϰ嵽��������ѡ���ס�������Ʒ�Ƶ�ˮ������������Ϊ3Ԫ���ҽ�������Ϊ4Ԫ�����Ǹ������أ�Ԥ�ƹ�����Ʒ��ˮ��������y���������Ʒ��ˮ��������x������֮��ĺ�����ϵ��ͼ��ʾ��
��1������ͼ����y��x֮��ĺ�����ϵʽ��
��2�����ó���ÿ����1����ˮ���ɻ���0.5Ԫ��ÿ����1����ˮ���ɻ���1Ԫ����д������W��Ԫ����x�������ĺ�����ϵʽ��
��3���ڣ�2���������£������ϰ�����ò�����700Ԫ�����ס�������Ʒ�Ƶ�ˮ������������Ʒ�Ƶ�ˮ��ȫ���۳������������149Ԫ���ʸó����м��ֽ������������ַ�����ʹ�������������Ϊ����Ԫ��

���𰸡���1��y=-x+200����2��W=-0.5x+200����3�� ����100ʱ�������=150Ԫ.
�������������������1�����ݺ���ͼ���ɴ���ϵ�����Ϳ���ֱ�����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2��1����ˮ���ɻ���0.5Ԫ��ÿ����1����ˮ���ɻ���1Ԫ���Ӷ��õ�����![]() ��
��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
��3�����Ʒ�ƽ���![]() ��������Ʒ�ƵĽ���
��������Ʒ�ƵĽ���![]() ��������������������ʽ�������⼴�ɣ�
��������������������ʽ�������⼴�ɣ�
�����������1����![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() �ɺ���ͼ��
�ɺ���ͼ��![]()
��ã� ![]()
��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
��2����![]()
1����ˮ���ɻ���0.5Ԫ��ÿ����1����ˮ���ɻ���1Ԫ��
![]()
��3�����Ʒ�ƽ���![]() ��������Ʒ�ƵĽ���
��������Ʒ�ƵĽ���![]() ���������⣬��
���������⣬��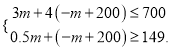
��ã� ![]()
��![]() ������
������![]()
���3�ֽ���������
����1����Ʒ�ƽ���100��������Ʒ�ƵĽ���100����
����2����Ʒ�ƽ���101��������Ʒ�ƵĽ���99����
����3����Ʒ�ƽ���102��������Ʒ�ƵĽ���98����![]()
��![]() ��
��![]() �����������
�����������
��![]() ʱ��
ʱ�� ![]() ���=150Ԫ��
���=150Ԫ��

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�