��Ŀ����
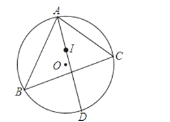
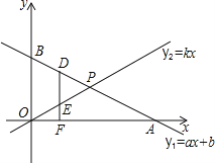
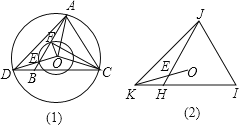
����Ŀ���۲췢�֣���ͼ��1������O����ADC�����Բ����B�DZ�CD�ϵ�һ�㣬����ABC�ǵȱ������Σ�OD��AB���ڵ�E����OΪԲ�ġ�OEΪ�뾶��Բ��AB�ڵ�F������CF��OF��
��1������AOD�Ķ�����
��2���߶�AE��CF�кδ�С��ϵ��֤����IJ��룮
��չӦ�ã���ͼ��2������HJI�ǵȱ������Σ���K��IH�ӳ����ϵ�һ�㣮��O����JKI�����ԲԲ�ģ�OK��JH�ཻ�ڵ�E������ȱ���������JHI�ı߳�Ϊ2����ֱ��д��JE����Сֵ�ʹ�ʱ��JEO�Ķ�����
���𰸡��۲췢������1����AOD=120�㣻��2��������AE=CF�����ɼ���������չӦ�ã� JE����СֵΪ![]() ����ʱ��JEO=45�㣮
����ʱ��JEO=45�㣮
��������
�۲췢�֣���1������Բ�ܽǶ������ɽ�����⣻
��2�����ۣ�AE=CF����취֤����AOE�ա�COF���ɣ�
��չӦ�ã���OΪԲ�ģ���OE��Ϊ�뾶��Բ����JH��F������IF���������Ͻ��ۿɵã�JE=IF�����ݴ��߶���̼��ɽ�����⣻
�⣺
�۲췢�֣���1���ߡ�ABC�ǵȱ������Σ�
���ACB=60�㣬
���AOD=2��ACB=120��
��2�����ۣ�AE=CF��
�������£��ߡ�AOD=120�㣬
���OEF+��OAF=60�㣬
�ߡ�OAC+��OAF=60�㣬
���OEF=��OAC��
��OE=OF��OA=OC��
���OEF=��OFE=��OAC=��OCA��
���EOF=��AOC��
���EOF+��AOF=��AOC+��AOF��
���AOE=��COF��
���AOE�ա�COF��
��AE=CF��
��չӦ�ã���OΪԲ�ģ���OE��Ϊ�뾶��Բ����JH��F������IF���������Ͻ��ۿɵã�JE=IF��
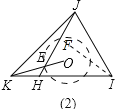
��IF��JHʱIF��С��IF=JIsin60��=2��![]() =
=![]() ��
��
�ߡ�FJO=��OIF����FGJ=��OGI��
���JOI=��JFI=90�㣬
���OJI=45�㣬
���JEO=��OJI=45�㣬
��JE����СֵΪ![]() ����ʱ��JEO=45�㣮
����ʱ��JEO=45�㣮