题目内容
【题目】直线y=2x﹣2与x轴交于点A,与y轴交于点B.
(1)求点A、B的坐标;
(2)点C在x轴上,且S△ABC=3S△AOB , 直接写出点C坐标.
【答案】
(1)解:令y=2x﹣2中y=0,则2x﹣2=0,解得:x=1,
∴A(1,0).
令y=2x﹣2中x=0,则y=﹣2,
∴B(0,﹣2).
(2)解:依照题意画出图形,如图所示.
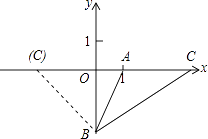
设点C的坐标为(m,0),
S△AOB= ![]() OAOB=
OAOB= ![]() ×1×2=1,S△ABC=
×1×2=1,S△ABC= ![]() ACOB=
ACOB= ![]() |m﹣1|×2=|m﹣1|,
|m﹣1|×2=|m﹣1|,
∵S△ABC=3S△AOB,
∴|m﹣1|=3,
解得:m=4或m=﹣2,
即点C的坐标为(4,0)或(﹣2,0).
【解析】(1)首先分别令y=2x-2中x=0、y=0,从而可求出与之对应的y、x值,故此可得出点A、B的坐标;
(2)首先设点C的坐标为(m,0),然后根据三角形的面积公式结合两三角形面积间的关系得出关于m含绝对值符号的一元一次方程,最后,解关于m的一元一次方程即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目