��Ŀ����
����Ŀ�����ǰ���ƽ���ı��������ֱ�߳�Ϊ�����ߡ��������������ͼ�����Եõ��ı��εġ����ߡ�����ͼ1�ı���ABCD�У�ȡ�Խ���BD���е�O������OA��OC����Ȼ������AOC��ƽ���ı���ABCD��������ٹ���O��OE��AC��CD��E����ֱ��AE��Ϊһ�������ߡ���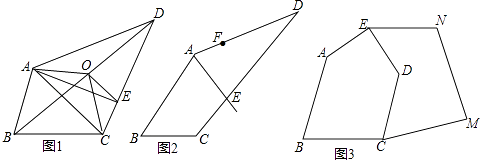
��1����ͼ1����˵��ֱ��AE�ǡ����ߡ������ɣ�
��2����ͼ2��AEΪһ�������ߡ���FΪAD���ϵ�һ�㣬����������F��ġ����ߡ�����˵�����ɣ�
��3����ͼ3�������ABCDE��һ�����ص�ʾ��ͼ���������꿪�ѻĵأ����ѱ����ͼ3��ʾ����״����ԭ�������뿪�ѻĵصķֽ�С·������CDE���������ţ����������E����һ��ֱ·��Ҫ��ֱ·��ߵ����������ԭ��һ���ֻࣨ�����ͼ�ʵ�˵������˵�����ɣ�
���𰸡�
��1���⣺�ߵ�O��BD���е㣬
��S��AOB=S��AOD��S��BOC=S��DOC��
��S��AOB+S��BOC=S��AOD+S��DOC= ![]() S�ı���ABCD��
S�ı���ABCD��
��S�ı���ABCO= ![]() S�ı���ABCD��
S�ı���ABCD��
������AOC��ƽ���ı���ABCD�������
��AE��OC��F��
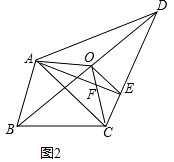
��OE��AC��
��S��AOE=S��COE��
��S��AOF=S��CEF��
������AOC��ƽ���ı���ABCD�������
��ֱ��AEƽ���ı���ABCD���������AE���ı���ABCD��һ�������ߡ���
��2���⣺����EF����A��EF��ƽ���߽�CD�ڵ�G������FG����GFΪһ�������ߡ���

��AG��EF��
��S��AGE=S��AFG��
��AE��FG�Ľ�����O����S��AOF=S��GOE��
��AEΪһ�������ߡ�������GFΪһ�������ߡ���
��3���⣺��ͼ3��
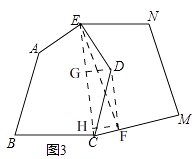
����CE������D��DF��EC��CM��F������EF����EFΪ����ֱ·��
���ɣ�����D��DG��CE��G������F��FH��EC��H��
��DF��EC����DG=FH������ƽ����ľ��봦����ȣ���
��S��CDE= ![]() EC��DG��S��CEF=
EC��DG��S��CEF= ![]() EC��FH��
EC��FH��
��S��CDE=S��CEF��
��S�ı���ABCDE=S�ı���ABCE+S��CDE=S�ı���ABCE+S��CEF=S�����ABCFE��
����ֱ·��ߵ����������ԭ��һ���࣮
����������1��������AH��BC������ΪH�����������ε������ʽ�ɵõ�S��ABD=![]() BDAH��S��ADC=
BDAH��S��ADC=![]() DCAH��Ȼ��������BD=CD���ɵõ�S��ABD=S��ADC�����жϳ�S�ı���ABCO=
DCAH��Ȼ��������BD=CD���ɵõ�S��ABD=S��ADC�����жϳ�S�ı���ABCO=![]() S�ı���ABCD�������жϳ�S��AOE=S��COE���Ƴ�S��AOF=S��CEF�������Ƴ�ֱ��AEƽ���ı���ABCD�������
S�ı���ABCD�������жϳ�S��AOE=S��COE���Ƴ�S��AOF=S��CEF�������Ƴ�ֱ��AEƽ���ı���ABCD�������
��2����������EF��FG��Ȼ�����A��EF��ƽ���߽�CD�ڵ�G����AG��EF���Ƴ�S��AGE=S��AFG����AE��FG�Ľ�����O����S��AOF=S��GOE����AEΪһ�������ߡ�������GFΪһ�������ߡ���
��3����������CE��EF��Ȼ�����D��DF��EC��CM��F��Ȼ�����ݼ���ƽ����ľ��봦����ȵó�DG=FH�����ǿɵõ�S��CDE=S��CEF.
�����㾫����������Ҫ������ƽ����֮��ľ�������֪ʶ�㣬��Ҫ��������ƽ���ߵľ��룺����ֱ��ƽ�У���һ��ֱ���ϵ�����һ������һ��ֱ�������ߣ����߶εij��ȣ���������ƽ���ߵľ��������ȷ�����⣮

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�