题目内容
 如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,BF=DE,
如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,BF=DE,
求证:(1)∠A=∠C
(2)AE∥CF.
证明:(1)∵AB∥CD(已知),
∴∠B=∠D(两直线平行,内错角相等);
又∵BF=DE(已知),
∴BF-EF=DE-EF,即BE=DF,
∴在△ABE和△CDF中,
 ,
,
∴△ABE≌△CDF(SAS),
∴∠A=∠C(全等三角形的对应角相等);
(2)由(1)知,△ABE≌△CDF,
∴∠BEA=∠DFC(全等三角形的对应角相等),
∴AE∥CF(内错角相等,两直线平行).
分析:(1)根据平行线的性质、线段间的和差关系证得∠B=∠D、BE=DF;然后由全等三角形的判定定理SAS推知△ABE≌△CDF;最后由全等三角形的对应角相等证得结论;
(2)利用(1)中全等三角形△ABE≌△CDF的对应角∠BEA=∠DFC,由内错角相等,两直线平行可以证得AE∥CF.
点评:本题考查了全等三角形的判定与性质、平行线的判定与性质.SSS,SAS,ASA,AAS,HL均可作为判定三角形全等的定理. 注意:在全等的判定中,没有AAA(角角角)和SSA(边边角)(特例:直角三角形为HL,因为勾股定理,只要确定了斜边和一条直角边,另一直角边也确定,属于SSS),因为这两种情况都不能唯一确定三角形的形状.
∴∠B=∠D(两直线平行,内错角相等);
又∵BF=DE(已知),
∴BF-EF=DE-EF,即BE=DF,
∴在△ABE和△CDF中,
 ,
,∴△ABE≌△CDF(SAS),
∴∠A=∠C(全等三角形的对应角相等);
(2)由(1)知,△ABE≌△CDF,
∴∠BEA=∠DFC(全等三角形的对应角相等),
∴AE∥CF(内错角相等,两直线平行).
分析:(1)根据平行线的性质、线段间的和差关系证得∠B=∠D、BE=DF;然后由全等三角形的判定定理SAS推知△ABE≌△CDF;最后由全等三角形的对应角相等证得结论;
(2)利用(1)中全等三角形△ABE≌△CDF的对应角∠BEA=∠DFC,由内错角相等,两直线平行可以证得AE∥CF.
点评:本题考查了全等三角形的判定与性质、平行线的判定与性质.SSS,SAS,ASA,AAS,HL均可作为判定三角形全等的定理. 注意:在全等的判定中,没有AAA(角角角)和SSA(边边角)(特例:直角三角形为HL,因为勾股定理,只要确定了斜边和一条直角边,另一直角边也确定,属于SSS),因为这两种情况都不能唯一确定三角形的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
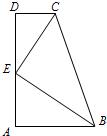 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.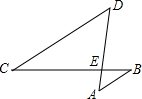 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=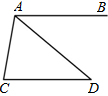 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.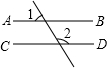 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )