题目内容
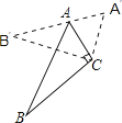
【题目】如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为______．
【答案】64°
【解析】
先利用互余计算出∠BAC=58°，再利用旋转的性质得CA=CA′，∠A′=∠BAC=58°，∠ACA′等于旋转角，根据等腰三角形的性质和三角形内角和计算出∠ACA′的度数即可．
解：∵∠ACB=90°，∠ABC=32°，
∴∠BAC=58°，
∵以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，
∴CA=CA′，∠A′=∠BAC=58°，∠ACA′等于旋转角，
∴∠CAA′=∠A′=58°，
∴∠ACA′=180°-58°-58°=64°，
即旋转角的度数为64°．
故答案为：64°．
练习册系列答案
相关题目
【题目】为了保护环境，某集团决定购买
、
两种型号的污水处理设备共10台，其中每台价格及月处理污水量如下表：
|
| |
价格（万元/元） | 15 | 12 |
处理污水量（吨/月） | 250 | 220 |
经预算，该集团准备购买设备的资金不高于130万元.
（1）请你设计该企业有哪几种购买方案？
（2）试通过计算，说明哪种方案处理污水多？
