题目内容
【题目】已知函数y=mx2+(2m+1)x+2(m为实数). 
(1)请探究该函数图象与x轴的公共点个数的情况(要求说明理由);
(2)在图中给出的平面直角坐标系中分别画出m=﹣1和m=1的函数图象,并根据图象直接写出它们的交点坐标;
(3)探究:对任意实数m,函数的图象是否一定过(2)中的点,并说明理由.
【答案】
(1)解:当m=0时,y=x+2,此直线与x轴交于(﹣2,0);
当m≠0时,△=(2m+1)2﹣8m=(2m﹣1)2≥0,
∴此抛物线在m= ![]() 时,与x轴只有一个公共点;在m≠
时,与x轴只有一个公共点;在m≠ ![]() 时,与x轴有2个交点
时,与x轴有2个交点
(2)解:当m=﹣1时,抛物线解析式为y=﹣x2﹣x+2,
当m=1时,抛物线解析式为y=x2+3x+2,
函数图象如下:
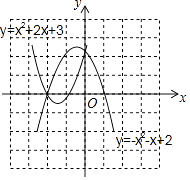
由函数图象知,两抛物线的交点为(﹣2,0)和(0,2)
(3)解:对任意实数m,函数的图象一定过(﹣2,0)和(0,2),理由如下:
在函数y=mx2+(2m+1)x+2中,
无论m为何值,当x=0时,y的值均为2,即横过点(0,2),
∵y=mx2+(2m+1)x+2=(x+2)(mx+1),
∴当x=﹣2时,y的值均为0,即函数图象横过(﹣2,0),
故无论m为何值,函数的图象(﹣2,0)和(0,2)两点
【解析】(1)分m=0和m≠0两种情况讨论;(2)m=﹣1时y=﹣x2﹣x+2、m=1时y=x2+3x+2,画出函数图象,根据函数图象得出交点;(3)在y=mx2+(2m+1)x+2=(x+2)(mx+1)中,可知无论m为何值,x=0时y=2、x=﹣2时y=0,即可得.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 16 | 50 |
4 | 20 | 70 |
5 | m | 不低于36元且不超过95元 |
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.