��Ŀ����
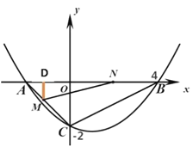
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+6������A����3��0���͵�B��2��0����ֱ��y=h��hΪ��������0��h��6����BC���ڵ�D����y�ύ�ڵ�E����AC���ڵ�F�����������ڵڶ������ڵ�G��
��1���������ߵĽ���ʽ��
��2������BE����hΪ��ֵʱ����BDE��������
��3����֪һ����M����2��0�����ʣ��Ƿ����������ֱ��y=h��ʹ��OMF�ǵ��������Σ������ڣ������h��ֵ�͵�G�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1�� y=-x2-x+6����2�� ��h=3ʱ����BDE����������������![]() ����3�� ����������ֱ��y=2��y=4��ʹ��OMF�ǵ��������Σ���h=4ʱ����G������Ϊ��-2��4������h=2ʱ����G������Ϊ��
����3�� ����������ֱ��y=2��y=4��ʹ��OMF�ǵ��������Σ���h=4ʱ����G������Ϊ��-2��4������h=2ʱ����G������Ϊ��![]() ��2����
��2����
��������
��1���ѵ�A��B������ֱ���������߽���ʽ���г�����ϵ��a��b�Ľ���ʽ��ͨ���ⷽ����������ǵ�ֵ���ɵø�����������Ӧ�ĺ�����ϵʽ��
��2����õ�C�����꣬�����ֱ��BC�ĺ�����ϵʽ����h��ʾ��DE�ij������������ε������ʽ���������BDE�������hΪ�����Ķ��κ���ģ�ͣ����ö��κ�����������⼴�ɣ�
��3����OF=FM��OF=OM��FM=OM���������⼴��.
��1���� ������y=ax2+bx+6������A(-3,0)�͵�B(2,0)��
��![]()
���![]()
�� ������������Ӧ�ĺ�����ϵʽΪy=-x2-x+6.
��2����ͼ��
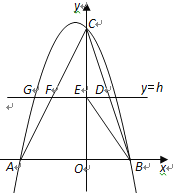
�� ������y=-x2-x+6��y�ύ�ڵ�C���� C(0,6).
��ֱ��BC�ĺ�����ϵʽΪy=k1x+b1���� y=-3x+6.
��y=hʱ��-3x+6=h����![]() ����
����![]() .
.
�� ![]() .
.
�� ��h=3ʱ����BDE��������.
��3����ͼ2.2����ֱ��AC�ĺ�����ʽΪy=k2x+b2��
�� y=2x+6.
��y=hʱ��2x+6=h����![]() ��
��
�� F(![]() h-3,h),
h-3,h),
�� ![]() .
.
�֡� M(-2,0)��
�� OM2=4��FM2=(![]() h-3+2)2+ h2=(
h-3+2)2+ h2=(![]() h-1)2+ h2.
h-1)2+ h2.
�� ��OF=FM����(![]() h-3)2+ h2=(
h-3)2+ h2=(![]() h-1)2+ h2��
h-1)2+ h2��
���h=4.
(���⣺�ɵ��������������ߺ�һ����
��![]() -3=-1����h=4.)
-3=-1����h=4.)
��-x2-x+6=4�����x1=-2��x2=1(��ȥ)��
�� G(-2,4).
�� ��OF=OM����(![]() h-3)2+ h2=4��������ʵ����.
h-3)2+ h2=4��������ʵ����.
�� ��FM=OM����(![]() h-1)2+ h2=4�����h1=2��
h-1)2+ h2=4�����h1=2��![]() (��ȥ).
(��ȥ).
��-x2-x+6=2�����![]() ,
,![]() (��ȥ)��
(��ȥ)��
��G(![]() ,2).
,2).
��������������������ֱ��y=h��ʹ��OFM�ǵ��������Σ���ʱh=4��G(-2,4)��h=2��G(![]() ,2).
,2).

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�