题目内容
如图,在平面直角坐标系中,已知OB=2,点A和点B关于N(0,-2)成中心对称,抛物线y=ax2+bx+c经过点A、O、B三点.
(1)求抛物线的函数表达式;
(2)若点P是x轴上的一动点,从点O出发沿射线OB方向运动,圆P半径为
,速度为每秒1个单位,试求几秒后圆P与直线AB相切;
(3)在此抛物线上,是否存在点P,使得以点P与点O、A、B为顶点的四边形是梯形?若存在,求点P的坐标;若不存在,请说明理由.

(1)求抛物线的函数表达式;
(2)若点P是x轴上的一动点,从点O出发沿射线OB方向运动,圆P半径为
3
| ||
| 4 |
(3)在此抛物线上,是否存在点P,使得以点P与点O、A、B为顶点的四边形是梯形?若存在,求点P的坐标;若不存在,请说明理由.

(1)设点A的坐标为(x,y).
∵点A和点B(2,0)关于N(0,-2)成中心对称,
∴N为线段AB的中点,
∴
=0,
=-2,
解得x=-2,y=-4,
∴点A的坐标为(-2,-4).
∵抛物线y=ax2+bx+c经过A、O、B三点,
∴
,解得
,
∴抛物线的函数表达式为y=-
x2+x;
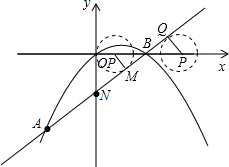 (2)如图,设x秒后圆P与直线AB相切,则OP=x.分两种情况:
(2)如图,设x秒后圆P与直线AB相切,则OP=x.分两种情况:
①点P在点B左边时,设圆P与直线AB切于点M,则∠BMP=90°,PM=
.
在△BMP与△BON中,
,
∴△BMP∽△BON,
∴
=
,即
=
,
解得x=
,
即
秒后圆P与直线AB相切;
②点P在点B右边时,设圆P与直线AB切于点Q,则∠BQP=90°,PQ=
.
在△BQP与△BON中,
,
∴△BQP∽△BON,
∴
=
,即
=
,
解得x=
,
即
秒后圆P与直线AB相切;
综上所述,
秒或
秒后圆P与直线AB相切;
(3)点P与点O、A、B为顶点的四边形是梯形时,分三种情况:
①当P1与A点关于抛物线对称轴对称时,OB∥AP1,AP1BO为梯形,此时P1(4,-4);
②设存在点P2,使OP2∥AB.
设直线AB的解析式为y=kx+m,
∵A(-2,-4),B(2,0),
∴
,解得
,
∴直线AB的解析式为y=x-2,
∴OP2的解析式为y=x.
由
,解得
,
∴P2(0,0),与原点O重合,不合题意,舍去;
③设存在点P3,使BP3∥OA.
设直线OA的解析式为y=nx,
∵A(-2,-4),
∴-2n=-4,解得n=2,
∴直线OA的解析式为y=2x,
∴BP3的解析式为y=2x-4.
由
,解得
,
∴P3(-4,-12),
综上所述,存在点P(4,-4)或(-4,-12),使得以点P与点O、A、B为顶点的四边形是梯形.
∵点A和点B(2,0)关于N(0,-2)成中心对称,
∴N为线段AB的中点,
∴
| x+2 |
| 2 |
| y+0 |
| 2 |
解得x=-2,y=-4,
∴点A的坐标为(-2,-4).
∵抛物线y=ax2+bx+c经过A、O、B三点,
∴
|
|
∴抛物线的函数表达式为y=-
| 1 |
| 2 |
 (2)如图,设x秒后圆P与直线AB相切,则OP=x.分两种情况:
(2)如图,设x秒后圆P与直线AB相切,则OP=x.分两种情况:①点P在点B左边时,设圆P与直线AB切于点M,则∠BMP=90°,PM=
3
| ||
| 4 |
在△BMP与△BON中,
|
∴△BMP∽△BON,
∴
| MP |
| ON |
| BP |
| BN |
| ||||
| 2 |
| 2-x | ||
2
|
解得x=
| 1 |
| 2 |
即
| 1 |
| 2 |
②点P在点B右边时,设圆P与直线AB切于点Q,则∠BQP=90°,PQ=
3
| ||
| 4 |
在△BQP与△BON中,
|
∴△BQP∽△BON,
∴
| PQ |
| ON |
| BP |
| BN |
| ||||
| 2 |
| x-2 | ||
2
|
解得x=
| 7 |
| 2 |
即
| 7 |
| 2 |
综上所述,
| 1 |
| 2 |
| 7 |
| 2 |
(3)点P与点O、A、B为顶点的四边形是梯形时,分三种情况:
①当P1与A点关于抛物线对称轴对称时,OB∥AP1,AP1BO为梯形,此时P1(4,-4);
②设存在点P2,使OP2∥AB.
设直线AB的解析式为y=kx+m,
∵A(-2,-4),B(2,0),
∴
|
|
∴直线AB的解析式为y=x-2,
∴OP2的解析式为y=x.
由
|
|
∴P2(0,0),与原点O重合,不合题意,舍去;
③设存在点P3,使BP3∥OA.
设直线OA的解析式为y=nx,
∵A(-2,-4),
∴-2n=-4,解得n=2,
∴直线OA的解析式为y=2x,
∴BP3的解析式为y=2x-4.
由
|
|
∴P3(-4,-12),
综上所述,存在点P(4,-4)或(-4,-12),使得以点P与点O、A、B为顶点的四边形是梯形.

练习册系列答案
相关题目
 B中点,点E是直线OC上的一个动点(点E与点O不重合),点D在y轴上,且EO=ED.
B中点,点E是直线OC上的一个动点(点E与点O不重合),点D在y轴上,且EO=ED.


 上,B点的坐标为(1,0).
上,B点的坐标为(1,0). 点C,B的横坐标,且此抛物线过点A(3,6).
点C,B的横坐标,且此抛物线过点A(3,6). ?(不超过30字)
?(不超过30字)