题目内容
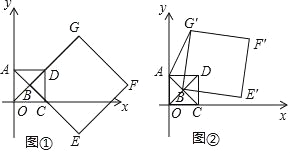
【题目】在平面直角坐标系中,O为坐标原点,点A(0,1),点C(1,0),正方形AOCD的两条对角线的交点为B,延长BD至点G,使DG=BD,延长BC至点E,使CE=BC,以BG,BE为邻边作正方形BEFG.
(Ⅰ)如图①,求OD的长及![]() 的值;
的值;
(Ⅱ)如图②,正方形AOCD固定,将正方形BEFG绕点B逆时针旋转,得正方形BE′F′G′,记旋转角为α(0°<α<360°),连接AG′.
①在旋转过程中,当∠BAG′=90°时,求α的大小;
②在旋转过程中,求AF′的长取最大值时,点F′的坐标及此时α的大小(直接写出结果即可).
【答案】(Ⅰ)![]() (Ⅱ)①α=30°或150°时,∠BAG′=90°②当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为
(Ⅱ)①α=30°或150°时,∠BAG′=90°②当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为![]() +2,此时α=315°,F′(
+2,此时α=315°,F′(![]() +
+![]() ,
,![]() ﹣
﹣![]() )
)
【解析】
(1)根据正方形的性质以及勾股定理即可解决问题,(2)①因为∠BAG′=90°,
BG′=2AB,可知sin∠AG′B=![]() ,推出∠AG′B=30°,推出旋转角α=30°,据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°,②当α=315°时,A、B、F′在一条直线上时,AF′的长最大.
,推出∠AG′B=30°,推出旋转角α=30°,据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°,②当α=315°时,A、B、F′在一条直线上时,AF′的长最大.
(Ⅰ)如图1中,
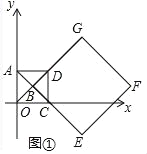
∵A(0,1),
∴OA=1,
∵四边形OADC是正方形,
∴∠OAD=90°,AD=OA=1,
∴OD=AC=![]() =
=![]() ,
,
∴AB=BC=BD=BO=![]() ,
,
∵BD=DG,
∴BG=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
(Ⅱ)①如图2中,
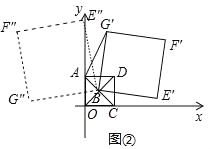
∵∠BAG′=90°,BG′=2AB,
∴sin∠AG′B=![]() =
=![]() ,
,
∴∠AG′B=30°,
∴∠ABG′=60°,
∴∠DBG′=30°,
∴旋转角α=30°,
根据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°,
综上所述,旋转角α=30°或150°时,∠BAG′=90°.
②如图3中,连接OF,
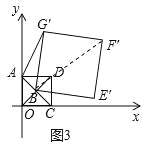
∵四边形BE′F′G′是正方形的边长为![]()
∴BF′=2,
∴当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为![]() +2,
+2,
此时α=315°,F′(![]() +
+![]() ,
,![]() ﹣
﹣![]() )
)