Question

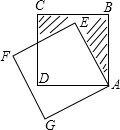
在Rt△ABC中，AC=BC，点D为AB中点．∠GDH=90°，∠GDH绕点D旋转，DG，DH分别与边AC，BC交于E，F两点．下列结论：①AE+BF=AC，②AE²+BF²=EF²，③S_{四边形CEDF}=

1

2

S_△ABC，④△DEF始终为等腰直角三角形．其中正确的是（　　）

A．①②③④

B．①②③

C．①④

D．②③

Answer 1

延长FD到M使MD=DF，连结AM、EM、CD，如图，
∵AC=BC，点D为AB中点．∠GDH=90°，
∴CD=BD，∠B=∠DCA=45°，CD⊥AB，
∵∠GDF=90°，即∠CDE+∠CDF=90°，
而∠CDF+∠BDF=90°，
∴∠CDE=∠BDF，
在△CDE和△BDF中，

∠DCE=∠B ∠CDE=∠BDF CD=BD

，
∴△CDE≌△BDF（AAS），
∴CE=BF，DE=DF，
∴AE+BF=AE+CE=AC，故①正确；
∵∠EDF=90°，
∴△DEF始终为等腰直角三角形，故④正确；
∵△CDE≌△BDF，
∴S_△CDE=S_△BDF，
∴S_{四边形CEDF}=S_△CDB=

1

2

S_△ABC，故③正确；
在△DAM和△DBF中，

DA=DB ∠ADM=∠BDF DM=DF

，
∴△DAM≌△DBF（SAS），
∴AM=BF，∠DAM=∠B=45°，
∴∠EAM=45°+45°=90°，
∴AE²+AM²=EM²，
∴AE²+BF²=EM²，
∵ED垂直平分MF，
∴EM=EF，
∴AE²+BF²=EF²，故②正确．
故选：A．