题目内容
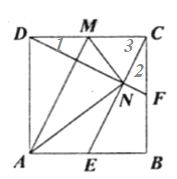
【题目】如图，E，F，M分别是正方形ABCD三边的中点，CE与DF交于N，连接AM，AN，MN对于下列四个结论：①AM∥CE；②DF⊥CE；③AN=BC；④∠AND=∠CMN． 其中错误的是（ ）
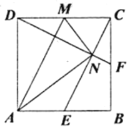
A.①B.②C.③D.④
【答案】D
【解析】
证四边形AECM为平行四边形得①正确，证
≌
(SAS)易得②正确，证AM垂直平分DN得到③正确，而推导不出∠AND=∠CMN，故④错误
解:∵正方形ABCD，M,E分别为DC，AB的中点，∴CM∥AE，CM=AE,∴四边形AECM为平行四边形，∴AM//CE，①正确；∵CD=BC,∠DCB=∠CBE=90°，CF=BE，∴≌(SAS)，∴∠1=∠2，∵∠2+∠3=90°，∴∠1+∠3=90°，∴DF⊥CE，∴②正确；∵Rt
,M为斜边DC的中点，∴DM=CM=MN，∵AM//CE，DF⊥CE，∴AM⊥DF，∴AM垂直平分DN，∴AD=AN=BC，∴③正确，∴∠AND=∠ADN，∵∠1+∠AND=90°，∠1+∠3=90°，∴∠AND=∠3=∠MNC≠∠CMN，故④错误.故答案为D.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
