题目内容
【题目】如图![]() ,在四边形ABCD的边AB上任取一点
,在四边形ABCD的边AB上任取一点![]() 点P不与A,B重合
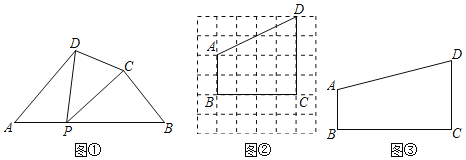
点P不与A,B重合![]() ,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.
,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.
解决问题
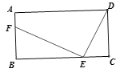
![]() 如图
如图![]() ,
,![]() ,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.
,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.
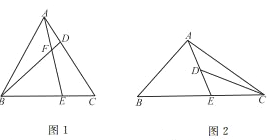
![]() 如图
如图![]() ,在四边形ABCD中,A,B,C,D四点均在正方形网格
,在四边形ABCD中,A,B,C,D四点均在正方形网格![]() 网格中每个小正方形的边长为
网格中每个小正方形的边长为![]() 的格点
的格点![]() 即每个小正方形的顶点
即每个小正方形的顶点![]() 上,试在图
上,试在图![]() 中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;
中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;
![]() 如图
如图![]() ,在四边形ABCD中,
,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() 点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.
点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.
【答案】![]() 结论:点P是四边形ABCD的边AB上的相似点,理由见解析;(2)画出四边形ABCD的边BC上的相似点,见解析;
结论:点P是四边形ABCD的边AB上的相似点,理由见解析;(2)画出四边形ABCD的边BC上的相似点,见解析;![]() ∽
∽![]() ,
,![]() ∽
∽![]() ;
;![]() .
.
【解析】
![]() 结论:点P是四边形ABCD的边AB上的相似点,根据相似点的定义判断即可.
结论:点P是四边形ABCD的边AB上的相似点,根据相似点的定义判断即可.
![]() 分两种情形分别求解即可.
分两种情形分别求解即可.
![]() 取AD的中点O,作
取AD的中点O,作![]() ,垂足为
,垂足为![]() 则点P为所求,连接AP,
则点P为所求,连接AP,![]() 证明点P是强相似点,求出AE即可解决问题.
证明点P是强相似点,求出AE即可解决问题.
:![]() 结论:点P是四边形ABCD的边AB上的相似点,
结论:点P是四边形ABCD的边AB上的相似点,
理由:如图![]() 中,
中,
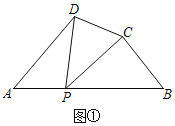
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() 点P是四边形ABCD的边AB上的相似点.
点P是四边形ABCD的边AB上的相似点.
![]() 如图
如图![]() 中,作
中,作![]() ,交边BC于点
,交边BC于点![]() ,则点
,则点![]() 为所求,此时
为所求,此时![]() ∽
∽![]() :
:
作点A关于直线BC的对称点A’:连接DA’,交BC于点![]() ,
,
则点![]() 为所求,此时
为所求,此时![]() ∽
∽![]() ,
,
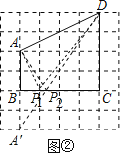
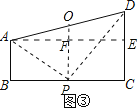
![]() 取AD的中点O,作
取AD的中点O,作![]() ,垂足为
,垂足为![]() 则点P为所求,连接AP,DP.
则点P为所求,连接AP,DP.
![]() ,
,![]() ,
,
![]() ,
,
作![]() ,则四边形ABCE,ABPF,FPCE均为矩形,
,则四边形ABCE,ABPF,FPCE均为矩形,
![]() ,
,![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
同理可证:![]() ,
,
![]() ,
,
![]() ∽
∽![]() ∽
∽![]() ,
,
![]() 点P是四边形ABCD的边BC上的一个强相似点,
点P是四边形ABCD的边BC上的一个强相似点,
在![]() 中,
中,![]() .
.
![]() ,
,
![]() .
.

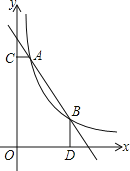
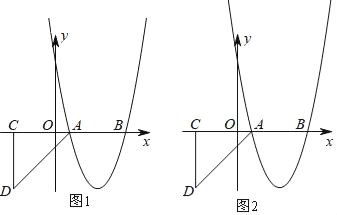
【题目】二次函数y=ax+bx+c(a,b,c为常数)中的x与y的部分对应值如表所示:
x | -1 | 0 | 1 | 3 |
y | | 3 |
| 3 |
下列结论:
(1)abc<0
(2)当x>1时,y的值随x值的增大而减小;
(3)16a+4b+c<0
(4)x=3是方程ax+(b-1)x+c=0的一个根;其中正确的个数为( )
A. 4个B. 3个C. 2个D. 1个