Question

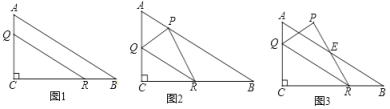
【题目】已知△ABC中，AB=AC，∠BAC=90°，D、E分别是AB、AC的中点，将△ADE绕点A按顺时针方向旋转一个角度α（0°＜α＜90°）得到△AD'E′，连接BD′、CE′，如图1．

（1）求证：BD′=CE'；

（2）如图2，当α=60°时，设AB与D′E′交于点F，求的值．

Answer 1

【答案】(1)详见解析;(2).

【解析】

（1）首先依据旋转的性质和中点的定义证明AD′=AE′，然后再利用SAS证明△BD′A≌△CE′A，最后，依据全等三角形的性质进行证明即可；

（2）连接DD′，先证明△ADD′为等边三角形，然后再证明△△ABD′为直角三角形，接下来，再证明△BFD′∽△AFE′，最后，依据相似三角形的性质求解即可．

（1）证明：∵AB=AC，D、E分别是AB、AC的中点，

∴AD=BD=AE=EC．

由旋转的性质可知：∠DAD′=∠EAE′=α，AD′=AD，AE′=AE．

∴AD′=AE′，

∴△BD′A≌△CE′A，

∴BD′=CE′．

（2）连接DD′．

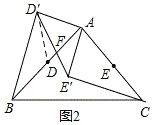
∵∠DAD′=60°，AD=AD′，

∴△ADD′是等边三角形．

∴∠ADD′=∠AD′D=60°，DD′=DA=DB．

∴∠DBD′=∠DD′B=30°，

∴∠BD′A=90°．

∵∠D′AE′=90°，

∴∠BAE′=30°，

∴∠BAE′=∠ABD′，

又∵∠BFD′=∠AFE′，

∴△BFD′∽△AFE′，

∴．

∵在Rt△ABD′中，tan∠BAD′=，

∴．