题目内容
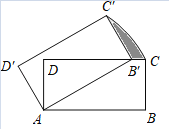
【题目】在矩形ABCD中,如图,AB=10,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
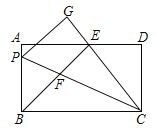
(1)求证:BP=BF;(2)当BP=8时,求BE·EF的值.
【答案】(1)见解析;(2) BE·EF=80.
【解析】
(1)利用折叠的性质,得出∠PGC=∠PBC=90°,∠BPC=∠GPC,进而判断出∠GPF=∠PFB即可得出结论;
(2)判断出△GEF∽△EAB,即可得出结论.
(1)在矩形ABCD中,∠ABC=90°,
∵△BPC沿P折叠得到△GPC,
∴∠PGC=∠PBC=90°,∠BPC=∠GPC,
∵BE⊥CG,
∴BE∥GP,
∴∠GPF=∠PFB,
∴∠BPF=∠BFP,
∴BP=BF;
(2)连接GF,
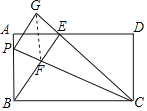
∵∠GEF=∠BAE=90°,
∵BF∥PG,BF=PG,
∴四边形BPGF是平行四边形,
∵BP=BF,
∴平行四边形BPGF是菱形,
∴BP∥GF,
∴∠GFE=∠ABE,
∴△GEF∽△EAB,
∴![]() ,
,
∴BE·EF=AB·GF=10×8=80.

练习册系列答案
相关题目