题目内容
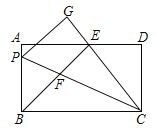
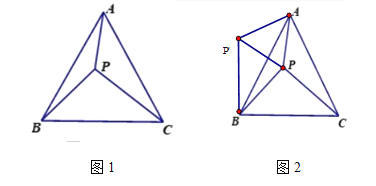
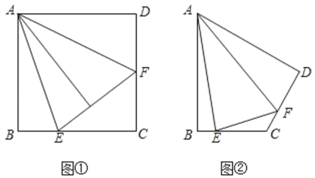
【题目】探究:如图①点E、F分别在正方形ABCD的边BC、CD上,连结AE、AF、EF,将△ABE、△ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形.若BE=2,DF=3,求AB的长;
拓展:如图②点E、F分别在四边形BACD的边BC、CD上,且∠B=∠D=90°.连结AE、AF、EF将△ABE、△ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形.若∠EAF=30°,AB=4,则△ECF的周长是 .
【答案】探究:AB=6;拓展:![]() .
.
【解析】
探究:设:正方形的边长为a,则EC=a-2,CF=a-3,则由勾股定理得:EF2=EC2+CF2,即可求解;
拓展:证明△ABC≌△ADC,∠BAE+∠DAF=∠EAF=30°,则∠BAD=60°,∠BAC=∠DAC=![]() (∠BAD)=30°,CD=BC=ABtan∠BAC,即可求解.
(∠BAD)=30°,CD=BC=ABtan∠BAC,即可求解.
探究:
设:正方形的边长为a,则EC=a﹣2,CF=a﹣3,
则EF=BE+DF=5,则EF2=EC2+CF2,
即:25=(a﹣2)2+(a﹣3)2,解得:a=6或﹣1(舍去﹣1),
故AB=6;
拓展:
由题意得:AB=CD=4,连接AC,
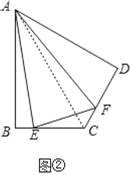
∵AB=CD,AC=AC,∴△ABC≌△ADC,
∴BC=CD,∠BAC=∠DAC,
∵点E、F分别在四边形BACD的边BC、CD上,
故:∠BAE+∠DAF=∠EAF=30°,则∠BAD=60°,
∴∠BAC=∠DAC=![]() (∠BAD)=30°,
(∠BAD)=30°,
CD=BC=ABtan∠BAC=4×![]() =
=![]() ,
,
△ECF的周长=EF+EC+FC=AE+FD+EC+FC=AC+CD=2CD=![]() ,
,
故答案为:![]() .
.

【题目】列方程组解应用题.
某校七年级学生在三月份参加了“学雷锋,献爱心”活动.活动中,1班,2班和3班的同学为希望小学的学生购买了学习用品:书包和词典.已知1班、2班购买的情况如下表:
书包(个) | 词典(本) | 累计花费(元) | |
七年级1班 | 3 | 2 | 124 |
七年级2班 | 2 | 3 | 116 |
活动中,3班购买了4个书包和6本词典,问:3班共花费了多少元?