题目内容
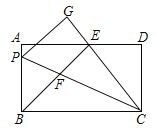
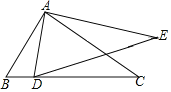
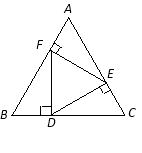
【题目】如图，在等边△ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，
FD⊥BC，则△DEF的面积与△ABC的面积之比等于（ ）
A．1∶3 B．2∶3 C．
∶2 D．
∶3
【答案】A．
【解析】
试题分析：∵DE⊥AC，EF⊥AB，FD⊥BC，
∴∠C+∠EDC=90°，∠FDE+∠EDC=90°，
∴∠C=∠FDE，
同理可得：∠B=∠DFE，∠A=DEF，
∴△DEF∽△CAB，
∴△DEF与△ABC的面积之比=（
）2，
又∵△ABC为正三角形，
∴∠B=∠C=∠A=60°，△EFD是等边三角形，
∴EF=DE=DF，
又∵DE⊥AC，EF⊥AB，FD⊥BC，
∴△AEF≌△CDE≌△BFD，
∴BF=AE=CD，AF=BD=DC，
在Rt△DEC中，
DE=DC×sin∠C=
DC，EC=cos∠C×DC=
DC，
又∵DC+BD=BC=AC=DC，
∴
∴△DEF与△ABC的面积之比等于：（
）2=1：3．
故答案选A．
【题目】“莓好河南，幸福家园”，2019年某省草莓旅游文化节期间，甲、乙两家草莓采摘园草莓品质相同，销售价格也相同，且推出了如下的优惠方案：
甲园 | 游客进园需购买20元/人的门票，采摘的草莓六折优惠 |
乙园 | 游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠 |
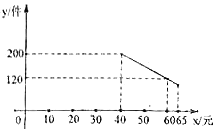
活动期间，小雪与爸爸妈妈决定选一个周末一同去采摘草莓，若设他们的草莓采摘量为x（千克）（出园时欲将自己采摘的草莓全部购买），在甲采摘园所需总费用为y1（元），在乙采摘园所需总费用为y2（元），图中折线OAB表示y2与x之间的函数关系．
（1）求y1、y2与x之间的函数关系式；
（2）请在图中画出y1与x之间大致的函数图象；
（3）若小雪和爸爸妈妈当天所采摘的草莓不少于10千克，则选择哪个草莓园更划算？请说明理由．
【题目】列方程组解应用题．
某校七年级学生在三月份参加了“学雷锋，献爱心”活动．活动中，1班，2班和3班的同学为希望小学的学生购买了学习用品：书包和词典．已知1班、2班购买的情况如下表：
书包（个） | 词典（本） | 累计花费（元） | |
七年级1班 | 3 | 2 | 124 |
七年级2班 | 2 | 3 | 116 |
活动中，3班购买了4个书包和6本词典，问：3班共花费了多少元？
