题目内容
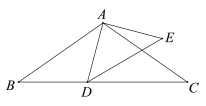
【题目】如图，在△ABC中，AB=AC，∠BAC=110°，△ADE的顶点D在BC上，且∠DAE=90°，AD=AE，则∠BAD-∠EDC的度数为（ ）
A.17.5°B.12.5°C.12°D.10°
【答案】D
【解析】
由AB=AC知∠B=∠C，据此得2∠B+∠BAC=180°，可知∠B=35°，根据∠DAE=90°、AD=AE知∠ADE=45°，利用∠BAD+∠B=∠ADE+∠EDC可得答案．
∵AB=AC，
∴∠B=∠C，
∴∠B+∠C+∠BAC=2∠B+∠BAC=180°，
又∵∠BAC=110°，
∴∠B=35°，
∵∠DAE=90°，AD=AE，
∴∠ADE=45°，
∵∠BAD+∠B=∠ADE+∠EDC
∴∠BAD-∠EDC =∠ADE-∠B=45°-35°=10°.
故选D．
新题型全程检测期末冲刺100分系列答案
【题目】“莓好河南，幸福家园”，2019年某省草莓旅游文化节期间，甲、乙两家草莓采摘园草莓品质相同，销售价格也相同，且推出了如下的优惠方案：
甲园 | 游客进园需购买20元/人的门票，采摘的草莓六折优惠 |
乙园 | 游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠 |
活动期间，小雪与爸爸妈妈决定选一个周末一同去采摘草莓，若设他们的草莓采摘量为x（千克）（出园时欲将自己采摘的草莓全部购买），在甲采摘园所需总费用为y1（元），在乙采摘园所需总费用为y2（元），图中折线OAB表示y2与x之间的函数关系．
（1）求y1、y2与x之间的函数关系式；
（2）请在图中画出y1与x之间大致的函数图象；
（3）若小雪和爸爸妈妈当天所采摘的草莓不少于10千克，则选择哪个草莓园更划算？请说明理由．
【题目】列方程组解应用题．
某校七年级学生在三月份参加了“学雷锋，献爱心”活动．活动中，1班，2班和3班的同学为希望小学的学生购买了学习用品：书包和词典．已知1班、2班购买的情况如下表：
书包（个） | 词典（本） | 累计花费（元） | |
七年级1班 | 3 | 2 | 124 |
七年级2班 | 2 | 3 | 116 |
活动中，3班购买了4个书包和6本词典，问：3班共花费了多少元？
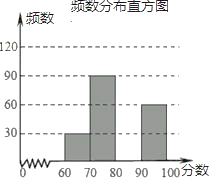
【题目】某校举行了”文明河南中小学生知识竞赛“活动，并随即抽查了部分同学的成绩，整理并制作成图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.1 |
70≤x＜80 | 90 | n |
80≤x＜90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |
请根据以上图表提供的信息，解答下列问题：
（1）请求出：m＝ ，n＝ ，抽查的总人数为 人；
（2）请补全频数分布直方图；
（3）抽查成绩的中位数应落在 分数段内；
（4）如果比赛成绩在80分以上（含80分）为优秀，任意抽取一位同学，则成绩优秀的概率为多少？
