题目内容
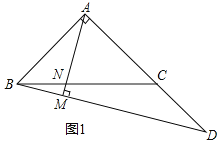
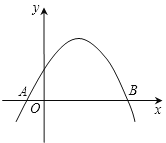
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
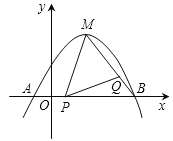
![]() 若抛物线的顶点为M,点P为线段OB上一动点
若抛物线的顶点为M,点P为线段OB上一动点![]() 不与点B重合
不与点B重合![]() ,点Q在线段MB上移动,且
,点Q在线段MB上移动,且![]() ,设线段
,设线段![]() ,
,![]() ,求
,求![]() 与x的函数关系式,并直接写出自变量x的取值范围;
与x的函数关系式,并直接写出自变量x的取值范围;
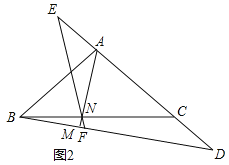
![]() 在同一平面直角坐标系中,两条直线
在同一平面直角坐标系中,两条直线![]() ,
,![]() 分别与抛物线交于点E、G,与
分别与抛物线交于点E、G,与![]() 中的函数图象交于点F、
中的函数图象交于点F、![]() 问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)m、n之间的数量关系是
;(3)m、n之间的数量关系是![]() 且
且![]() .
.
【解析】
![]() 将A、C的坐标代入抛物线的解析式中,即可求出
将A、C的坐标代入抛物线的解析式中,即可求出![]() 的函数解析式;
的函数解析式;
![]() 过M作
过M作![]() 轴于N,根据抛物线
轴于N,根据抛物线![]() 的函数解析式,即可得到M点的坐标,可分别在
的函数解析式,即可得到M点的坐标,可分别在![]() 和
和![]() 中,用勾股定理表示出MN的长,由此可得到关于PM、x的函数关系式;由于
中,用勾股定理表示出MN的长,由此可得到关于PM、x的函数关系式;由于![]() ,易证得
,易证得![]() ∽
∽![]() ,根据相似三角形得到的比例线段即可得到关于PM、
,根据相似三角形得到的比例线段即可得到关于PM、![]() 的关系式,联立两式即可求出
的关系式,联立两式即可求出![]() 、x的函数关系式;
、x的函数关系式;
![]() 根据两根抛物线的解析式和两条直线的解析式,可求出E、F、G、H四点的坐标,即可得到EF、GH的长,由于
根据两根抛物线的解析式和两条直线的解析式,可求出E、F、G、H四点的坐标,即可得到EF、GH的长,由于![]() ,若四边形EFHG是平行四边形,那么必有
,若四边形EFHG是平行四边形,那么必有![]() ,可据此求出m、n的数量关系.
,可据此求出m、n的数量关系.
解:![]() 抛物线
抛物线![]() 经过
经过![]() ,
,![]() 两点;
两点;
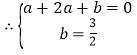 ,
,
解得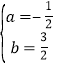 .
.
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
![]() 作
作![]() ,垂足为N.
,垂足为N.
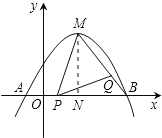
由![]() ,易得
,易得![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
根据勾股定理有:![]() ,
,
![]() ;
;
又![]() ,
,![]() 公共角
公共角![]() ,
,
![]() ∽
∽![]() ,
,
![]() ;
;
由![]() 得:
得:![]() ;
;
![]() ,
,
![]() 与x的函数关系式为
与x的函数关系式为![]() ;
;
![]() 四边形EFHG可以为平行四边形,m、n之间的数量关系是:
四边形EFHG可以为平行四边形,m、n之间的数量关系是:![]() 且
且![]() ;
;
![]() 点E、G是抛物线
点E、G是抛物线![]() 分别与直线
分别与直线![]() ,
,![]() 的交点,
的交点,
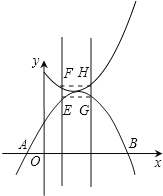
![]() 点E、G坐标为
点E、G坐标为![]() ,
,![]() ;
;
同理,点F、H坐标为![]() ,
,![]()
![]() ,
,![]() ;
;
![]() 四边形EFHG是平行四边形,
四边形EFHG是平行四边形,![]() ,
,
![]() ,
,
![]() ;
;
![]() 由题意知
由题意知![]() ,
,
![]() ;
;
因此四边形EFHG可以为平行四边形,m、n之间的数量关系是![]() 且
且![]() .
.

练习册系列答案
相关题目