题目内容
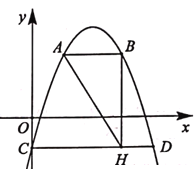
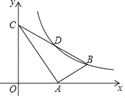
【题目】如图，在△ABC中，∠BAC＝90°，点A在x轴正半轴，点C在y轴正半轴，点D是边BC的中点，反比例函数
（k＞0，x＞0）的图象经过B，D．若点C的纵坐标为6，点D的横坐标为3.5，则k的值是（ ）
A. 6B. 8C. 12D. 14
【答案】D
【解析】
由题意可得C的坐标为（0，6），设D（3.5，
），由D是中点，可知点B的横坐标为7，纵坐标为
=
k﹣6，即点B的坐标为（7，k﹣6），代入反比例函数解析式求k即可.
解：∵点C的纵坐标为6，点D的横坐标为3.5，反比例函数
（k＞0，x＞0）的图象经过B，D．
∴C（0，6），D（3.5，），
∵点D是边BC的中点，
∴点B的坐标为（7，k﹣6），
∴7（k﹣6）＝k，
解得k＝14，
故选：D．
名校课堂系列答案
【题目】某医药研究所开发一种新的药物，据监测，如果成年人按规定的剂量服用，服药后2小时，每毫升血液中的含药量达到最大值，之后每毫升血液中的含药量逐渐衰减．若一次服药后每毫升血液中的含药量y（单位：微克）与服药后的时间t（单位：小时）之间近似满足某种函数关系，下表是y与t的几组对应值，其部分图象如图所示．
t | 0 | 1 | 2 | 3 | 4 | 6 | 8 | 10 | … |
y | 0 | 2 | 4 | 2.83 | 2 | 1 | 0.5 | 0.25 | … |
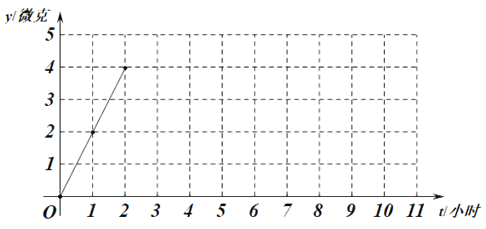
（1）在所给平面直角坐标系中，继续描出上表中已列出数值所对应的点（t，y），并补全该函数的图象；
（2）结合函数图象，解决下列问题：
①某病人第一次服药后5小时，每毫升血液中的含药量约为_______微克；若每毫升血液中含药量不少于0.5微克时治疗疾病有效，则第一次服药后治疗该疾病有效的时间共持续约_______小时；
②若某病人第一次服药后8小时进行第二次服药，第二次服药对血液中含药量的影响与第一次服药相同，则第二次服药后2小时，每毫升血液中的含药量约为_______微克．