题目内容
等腰直角三角形ABC的斜边BC的长为8,直线MN∥BC且与AB、AC分别交于M、N,将△AMN沿直线MN翻折得△A′MN,设△A′MN与△ABC重合部分面积为y,MN=x,(1)当A′在△ABC内部时,求y与x的函数关系式,并求x的取值范围;
(2)是否存在直线MN,使y的值为△ABC面积的
 ?若存在,求对应的x值;若不存在,说明理由.
?若存在,求对应的x值;若不存在,说明理由.
【答案】分析:(1)因为A′在ABC的内部,所以△A′MN的面积既是△AMN的面积,从而利用等腰直角三角形的性质即可得出y与x的函数关系式.
(2)先计算△ABC的面积,分情况进行讨论:①当A′在BC边上或在△ABC内部时,0<y≤4,根据(1)的函数关系式可作出判断;②当A′在△ABC外部时,求出梯形MNED的面积,结合题意可得出x的值,符合题意即存在,不符合则不存在.
解答:解:(1)y=S△A′MN= •
•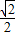 x•
x•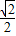 x=
x= x2(0<x<4);
x2(0<x<4);
(2)S△ABC= ×8×4=16,当A′在BC上时,x=4,y=4,
×8×4=16,当A′在BC上时,x=4,y=4,
∴①当A′在BC边上或在△ABC内部时,0<y≤4, 不在这个范围内,所以这时不存在直线MN.
不在这个范围内,所以这时不存在直线MN.
②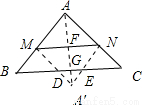 当A′在△ABC外部时,连AA′交MN于F,交BC于G,且A′F=AF=
当A′在△ABC外部时,连AA′交MN于F,交BC于G,且A′F=AF= x,
x,
∴FG=4- x,
x,
∴A′G= x-4+
x-4+ x=x-4,
x=x-4,
∴DE=2A′G=2x-8,
∴y= (x+2x-8)×(4-
(x+2x-8)×(4- x)=-
x)=- x2+8x-16(其中4<x<8),
x2+8x-16(其中4<x<8),
当y= 时,
时,
∵- x2+8x-16=
x2+8x-16=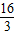 ,
,
即:(3x-16)2=0,
解为x1=x2=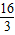 ,
,
∵4<x<8,
∴存在直线MN使重叠部分面积为△ABC面积的 ,
,
此时x=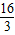 .
.
点评:本题考查翻折变换及等腰三角形的性质,综合性较强,难度较大,解答本题的关键是正确的画出示意图,利用所学的知识表示出重叠的面积,要求同学们熟练基础知识的掌握,此类综合题一般要求对基础知识比较熟悉才能解答出来.
(2)先计算△ABC的面积,分情况进行讨论:①当A′在BC边上或在△ABC内部时,0<y≤4,根据(1)的函数关系式可作出判断;②当A′在△ABC外部时,求出梯形MNED的面积,结合题意可得出x的值,符合题意即存在,不符合则不存在.
解答:解:(1)y=S△A′MN=
 •
•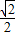 x•
x•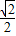 x=
x= x2(0<x<4);
x2(0<x<4);(2)S△ABC=
 ×8×4=16,当A′在BC上时,x=4,y=4,
×8×4=16,当A′在BC上时,x=4,y=4,∴①当A′在BC边上或在△ABC内部时,0<y≤4,
 不在这个范围内,所以这时不存在直线MN.
不在这个范围内,所以这时不存在直线MN.②
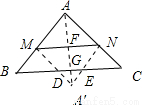 当A′在△ABC外部时,连AA′交MN于F,交BC于G,且A′F=AF=
当A′在△ABC外部时,连AA′交MN于F,交BC于G,且A′F=AF= x,
x,∴FG=4-
 x,
x,∴A′G=
 x-4+
x-4+ x=x-4,
x=x-4,∴DE=2A′G=2x-8,
∴y=
 (x+2x-8)×(4-
(x+2x-8)×(4- x)=-
x)=- x2+8x-16(其中4<x<8),
x2+8x-16(其中4<x<8),当y=
 时,
时,∵-
 x2+8x-16=
x2+8x-16=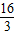 ,
,即:(3x-16)2=0,
解为x1=x2=
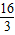 ,
,∵4<x<8,
∴存在直线MN使重叠部分面积为△ABC面积的
 ,
,此时x=
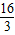 .
.点评:本题考查翻折变换及等腰三角形的性质,综合性较强,难度较大,解答本题的关键是正确的画出示意图,利用所学的知识表示出重叠的面积,要求同学们熟练基础知识的掌握,此类综合题一般要求对基础知识比较熟悉才能解答出来.

练习册系列答案
相关题目
 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
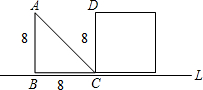 AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.
AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2. 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.