题目内容
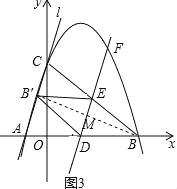
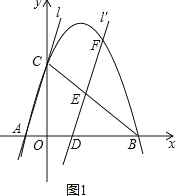
【题目】如图,在平面直角坐标系xoy中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位![]() 得到直线
得到直线![]() ,
, ![]() 交
交![]() 轴于点D,交BC于点E,交抛物线于点F.
轴于点D,交BC于点E,交抛物线于点F.
(1)求点![]() ,点
,点![]() 和点
和点![]() 的坐标
的坐标
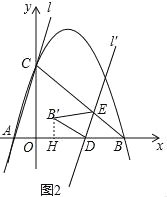
(2)如图2,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)在(2)的条件下,当点![]() 落在直线
落在直线![]() 上时,请直接写出点
上时,请直接写出点![]() 的坐标
的坐标

【答案】(1)A的坐标为(﹣2,0),点B的坐标为(8,0),点C的坐标为(0,6);
(2)点B′的坐标为(![]() m﹣10,﹣
m﹣10,﹣![]() m+6);
m+6);
(3)F的坐标为(![]() ﹣1,3
﹣1,3![]() ﹣12)
﹣12)
【解析】试题分析:(1)通过解方程![]() ,可得A点和B点坐标,再计算自变量为0时的函数值可得到C点坐标;(2)根据勾股定理求得BC=10,即可证得AB=BC,根据AC∥FD,得出
,可得A点和B点坐标,再计算自变量为0时的函数值可得到C点坐标;(2)根据勾股定理求得BC=10,即可证得AB=BC,根据AC∥FD,得出![]() ,求得BE=BD,即可证得四边形EB′DB是菱形,得出B′D∥BC,然后过点B′作B′H⊥AB与H,证得△B′HD∽△COB,即可求得
,求得BE=BD,即可证得四边形EB′DB是菱形,得出B′D∥BC,然后过点B′作B′H⊥AB与H,证得△B′HD∽△COB,即可求得![]() 进一步求得OH,得出B′的坐标;(3)根据菱形的性质得出BM=B′M,由平移的定义可知DE∥AC,根据平行线分线段成比例定理证得BD=AD=
进一步求得OH,得出B′的坐标;(3)根据菱形的性质得出BM=B′M,由平移的定义可知DE∥AC,根据平行线分线段成比例定理证得BD=AD=![]() AB=5,求得D的坐标,根据勾股定理求得AC的解析式,进而求得DF的解析式,然后联立方程,即可求得F的坐标.
AB=5,求得D的坐标,根据勾股定理求得AC的解析式,进而求得DF的解析式,然后联立方程,即可求得F的坐标.
试题解析:
(1)将y=0代入y=﹣![]() x2+
x2+![]() x+6得,﹣
x+6得,﹣![]() x2+
x2+![]() x+6=0,
x+6=0,
解得x1=﹣2,x2=8,
∴点A的坐标为(﹣2,0),点B的坐标为(8,0);
将x=0代入y=﹣![]() x2+
x2+![]() x+6得y=6,
x+6得y=6,
∴点C的坐标为(0,6);
(2)在RT△COB中,由勾股定理得BC=![]() ,
,
∵AB=AO+OB=2+8=10,
∴AB=BC,
∵AD=m,
∴DB=AB﹣AD=10﹣m,
∵AC∥FD,
∴![]() ,
,
∴BE=BD=B′E=B′D=10﹣m,
∴四边形EB′DB是菱形,
∴B′D∥BC,
过点B′作B′H⊥AB与H,
∴∠B′DH=∠CBO,∠B′HD=∠COB=90°,
∴△B′HD∽△COB,
∴![]() ,即
,即![]() ,
,
∴B′H=﹣![]() m+6,HD=﹣
m+6,HD=﹣![]() m+8,
m+8,
当点B′在y轴的右侧时,OH=OB﹣HD﹣DB=8﹣(﹣![]() m+8)﹣(10﹣m)=
m+8)﹣(10﹣m)=![]() m﹣10,
m﹣10,
当点B′在y轴的左侧时,OH=HD+DB﹣OB=(﹣![]() m+8)+(10﹣m)﹣8=10﹣
m+8)+(10﹣m)﹣8=10﹣![]() m,
m,
∴点B′的坐标为(![]() m﹣10,﹣
m﹣10,﹣![]() m+6);
m+6);
(3)∵四边形EB′DB是菱形,
∴BM=B′M,
由平移的定义可知DE∥AC,
∴![]() ,
,
∴BD=AD=![]() AB=5,
AB=5,
∵OA=2,
∴OD=3,
∴D的坐标为(3,0),
设直线AC的解析式为y=kx+b,
代入A(﹣2,0),C(0,6)得: ![]() ,解得
,解得![]() ,
,
∵DF∥AC,
设直线DF的解析式为y=3x+b,
代入D(3,0)得9+b=0,
解得b=﹣9,
∴直线DF为y=3x﹣9,
解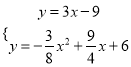 ,得
,得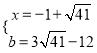 或
或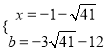 ,
,
∴F的坐标为(![]() ﹣1,3
﹣1,3![]() ﹣12).
﹣12).

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案

