题目内容
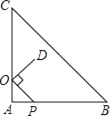
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
【答案】C
【解析】
根据题意,分顺时针旋转和逆时针旋转两种情况,求出点D′到x轴、y轴的距离,即可判断出旋转后点D的对应点D′的坐标是多少即可.
因为点D(6,4)在边AB上,
所以AB=BC=6,BD=6-4=2;
①若把△CDB顺时针旋转90°,
则点D′在x轴上,OD′=2,
所以D′(-2,0);
②若把△CDB逆时针旋转90°,
则点D′到x轴的距离为12,到y轴的距离为2,
所以D′(2,12),
综上,旋转后点D的对应点D′的坐标为(-2,0)或(2,12).
故选C.

练习册系列答案
相关题目