题目内容
正方形ABCD的边长为1,M为AB的中点,N为BC的中点,AN、CM相交于点O,则四边形AOCD的面积是
- A.

- B.

- C.

- D.
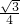
A
分析:利用锐角的正切值相等求出∠BAN=∠BCM,然后利用“角角边”证明△AMO和△CNO全等,根据全等三角形对应边相等可得OM=ON,再利用“SSS”证明△BOM与△BON全等,根据全等三角形的面积相等以及等底等高的三角形的面积相等可得S△AOM=S△BOM=S△BON=S△CON,再根据△ABN的面积求出△AOM的面积,然后用正方形的面积减去四部分三角形的面积,计算即可得解.
解答: 解:如图,连接OB,
解:如图,连接OB,
∵M为AB的中点,N为BC的中点,
∴AM=MB=CN=NB= ,
,
∴tan∠BAN=tan∠BCM= ,
,
∴∠BAN=∠BCM,
在△AMO和△CNO中,
∵ ,
,
∴△AMO≌△CNO(ASA),
∴OM=ON,
在△BOM和△BON中,
∵ ,
,
∴△BOM≌△BON(SSS),
又∵M、N是AB,AC的中点,
∴S△AOM=S△BOM=S△BON=S△CON,
∵S△ABN= ×1×
×1× =
= ,
,
∴S△AOM= ÷3=
÷3= ,
,
∴S四边形AOCD=1- ×4=
×4= .
.
故选A.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等底等高的三角形的面积相等,求出△BOM与△BON全等是解题的关键,作出图形更形象直观.
分析:利用锐角的正切值相等求出∠BAN=∠BCM,然后利用“角角边”证明△AMO和△CNO全等,根据全等三角形对应边相等可得OM=ON,再利用“SSS”证明△BOM与△BON全等,根据全等三角形的面积相等以及等底等高的三角形的面积相等可得S△AOM=S△BOM=S△BON=S△CON,再根据△ABN的面积求出△AOM的面积,然后用正方形的面积减去四部分三角形的面积,计算即可得解.
解答:
 解:如图,连接OB,
解:如图,连接OB,∵M为AB的中点,N为BC的中点,
∴AM=MB=CN=NB=
 ,
,∴tan∠BAN=tan∠BCM=
 ,
,∴∠BAN=∠BCM,
在△AMO和△CNO中,
∵
 ,
,∴△AMO≌△CNO(ASA),
∴OM=ON,
在△BOM和△BON中,
∵
 ,
,∴△BOM≌△BON(SSS),
又∵M、N是AB,AC的中点,
∴S△AOM=S△BOM=S△BON=S△CON,
∵S△ABN=
 ×1×
×1× =
= ,
,∴S△AOM=
 ÷3=
÷3= ,
,∴S四边形AOCD=1-
 ×4=
×4= .
.故选A.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等底等高的三角形的面积相等,求出△BOM与△BON全等是解题的关键,作出图形更形象直观.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 附加题
附加题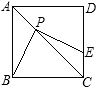 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
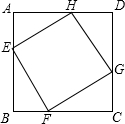
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3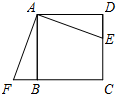 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=