题目内容
已知:如图①,在Rt△ACB中,∠C=90º,AC=6cm,BC=8cm,点P由B出发沿BC方向向点C匀速运动,速度为2cm/s;点Q由A出发沿AB方向向点B匀速运动,速度为1cm/s;连接PQ.若设运动的时间为t(s)(0<t<4),解答下列问题:

(1)当t为何值时,PQ的垂直平分线经过点B?
(2)如图②,连接CQ.设△PQC的面积为y(cm2),求y与t之间的函数关系式;
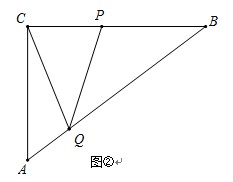
(3)如图②,是否存在某一时刻t,使线段C Q恰好把四边形ACPQ的面积分成1:2的两部分?若存在,求出此时t的值;若不存在,说明理由.
(1)当t= 时,PQ的垂直平分线经过点B;
时,PQ的垂直平分线经过点B;
(2)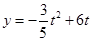 ;
;
(3)存在,当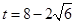
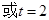 时,线段C Q恰好把四边形ACPQ的面积分成1:2的两部分.
时,线段C Q恰好把四边形ACPQ的面积分成1:2的两部分.
【解析】
试题分析:(1)用含有t的代数式表示PB和BQ,再根据线段垂直平分线上的点到线段两段点的距离相等即可;
(2)先证△BQH∽△BAC,再根据相似三角形的对应边成比例即可;
(3)分两种情况讨论:当S△AQC=2S△PQC时和当2S△AQC =S△PQC时,分别求出t的值.
试题解析:(1)在Rt△ABC中,AB=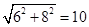 .
.
∵PQ的垂直平分线经过点B
∴PB=BQ
∵PB=2t,PQ=10-t,
∴2t=10-t
解得:t=
即:当t= 时,PQ的垂直平分线经过点B;
时,PQ的垂直平分线经过点B;
(2) 如图①过点Q作QH⊥BC于H.

∵∠C=90°,
∴AC⊥BC,
∴QH∥AC,
∴△BQH∽△BAC,
∴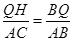 ,
,
∴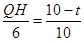 ,
,
∴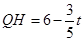 ,
,
∴ .
.
(3)存在
如图②过点Q作QM⊥BC于M,QN⊥AC于N,
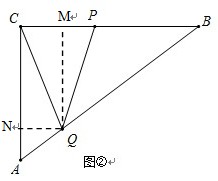
∵QM⊥BC于M,∠ACB=90°,
∴QM∥AC,
∴△BQM∽△BAC,
∴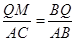 ,
,
∴ ,
,
∴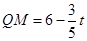 ,
,
∵QN⊥AC于N,∠ACB=90°,
∴QN∥BC,
∴△AQN∽△ABC,
∴ ,
,
∴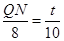 ,
,
∴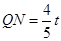 ,
,
∵线段CQ恰好把四边形ACPQ的面积分成1:2的两部分,
∴S△AQC=2S△PQC或2S△AQC =S△PQC
当S△AQC=2S△PQC时,
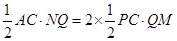
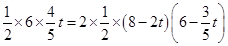
∴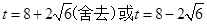
当2S△AQC =S△PQC时,
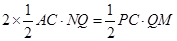

∴
综上可知:当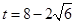
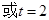 时,线段C Q恰好把四边形ACPQ的面积分成1:2的两部分.
时,线段C Q恰好把四边形ACPQ的面积分成1:2的两部分.
考点:三角形综合.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.