Question

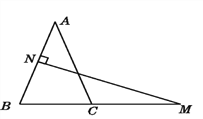
【题目】对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G1、G2的“密距”.例如，如上图，，，，则点A与射线OC之间的“密距”为，点B与射线OC之间的“密距”为3，如果直线y＝x-1和双曲线之间的“密距”为，则k值为（ ）

A. k=4 B. k=－4 C. k=6 D. k=－6

Answer 1

【答案】B

【解析】分析：由题意设双曲线上的D到直线的距离最近，过D作直线l和直线y=x-1的平行线，结合条件可求得l的解析式，联立l与双曲线解析式，则该方程组只有一组解，可求得k的值．

详解：

根据“密距”的定义可知双曲线图象在二、四象限，且离第四象限最近，
设双曲线上点D到直线y=x-1距离最近，如图，设直线y=x-1与y轴交于点E，过D作直线y=x-1的平行线，交y轴于点G，过D作直线y=x-1的垂线，垂足为E，过E作EH⊥DG，垂足为H，

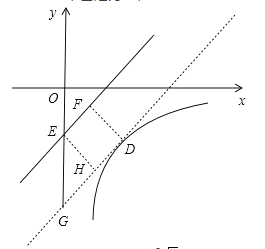
则由题意可知DF=EH=，

又∠OEF=45°，
∴∠EGH=45°，
∴EH=HG=，

∴EG=EH＝＝3，

又OE=1，

∴OG=4，

∴直线DG的解析式为y=x-4，

联立直线DG和双曲线解析式可得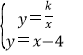 ，消去y整理可得x2-4x-k=0，
∵直线DG与双曲线只有一个交点，
∴方程x2-4x-k=0有两个相等的实数根，
∴△=0，即（-4）2+4k=0，解得k=-4，
故选B．