��Ŀ����
����Ŀ��������ȤС��ʱ����ʦ������������⣺
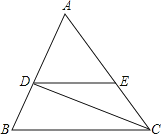
��1����ͼ1����ABC�У���AB=5��AC=3����BC���ϵ�����AD��ȡֵ��Χ��
С�������ھ��������������õ������µĽ��������
�ӳ�AD��E��ʹ��DE=AD��������BE������ACD�Ƶ�D��ʱ����ת180��õ���EBD������AB��AC��2AD��������ABE�У����������ε����߹�ϵ�ɵ�2��AE��8����1��AD��4��

������ʱ�������������֡��е㡱�����ߡ����������Կ��ǹ������е�Ϊ�Գ����ĵ����ĶԳ�ͼ�λ�ȫ�������Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬһ���������У�
��2����������
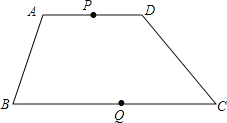
�ܵ���1��������������֤���������⣺��ͼ2������ABC�У�D��BC���ϵ��е㣬DE��DF��DE��AB�ڵ�E��DF��AC�ڵ�F������EF��
����֤��BE+CF��EF��������A=90�㣬̽���߶�BE��CF��EF֮��ĵ�����ϵ��������֤����
��3��������չ��
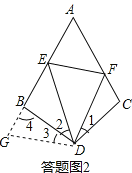
��ͼ3�����ı���ABDC�У���B+��C=180�㣬DB=DC����BDC=120�㣬��DΪ��������EDFΪ60��ǣ��ǵ����߷ֱ�AB��AC��E��F���㣬����EF��̽���߶�BE��CF��EF֮���������ϵ��������֤����
���𰸡�������
��������
�����������2���������ӳ�FD��G��ʹ��DG=DF�������ó�CF=BG��DF=DG���Լ�EF=EG�����������������߹�ϵ�ó��𰸣�
���ɢ�֪��FCD=��DBG��EF=EG�������ù��ɶ����ó��𰸣�
��3������ȫ�������ε��ж������ʵó���DEG�ա�DEF��SAS���������ó�EF=EG=BE+BG����EF=BE+CF�������ó��𰸣�
��2��֤�����������ͼ1���ӳ�FD��G��ʹ��DG=DF������BG��EG��
��CF=BG��DF=DG��
��DE��DF����EF=EG��
����BEG��BE+BG��EG����BE+CF��EF��
�⣺������A=90�㣬����EBC+��FCB=90�㣬
�ɢ�֪��FCD=��DBG��EF=EG��
���EBC+��DBG=90�㣬����EBG=90�㣬
����Rt��EBG��BE2+BG2=EG2��
��BE2+CF2=EF2��
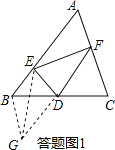
��3���⣺�����ͼ2������DCF�Ƶ�D��ʱ����ת120��õ���DBG��
�ߡ�C+��ABD=180�㣬��4=��C��
���4+��ABD=180�㣬
����E��B��G��ͬһֱ���ϣ�
�ߡ�3=��1����BDC=120�㣬��EDF=60�㣬
���1+��2=60�㣬����2+��3=60�㣬����EDG=60��
���EDF=��EDG=60�㣬
����DEG����DEF��
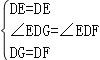
���DEG�ա�DEF��SAS����
��EF=EG=BE+BG����EF=BE+CF��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�