题目内容

【题目】如图，已知DE∥BC，CD是∠ACB的平分线，∠B=70°，∠ACB=50°，求∠EDC和∠BDC的度数．

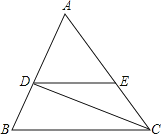
【答案】∠EDC=25°，∠BDC=85°

【解析】

试题分析：由CD是∠ACB的平分线，∠ACB=50°，根据角平分线的性质，即可求得∠DCB的度数，又由DE∥BC，根据两直线平行，内错角相等，即可求得∠EDC的度数，根据两直线平行，同旁内角互补，即可求得∠BDE的度数，即可求得∠BDC的度数．

解：∵CD是∠ACB的平分线，∠ACB=50°，

∴∠BCD=∠ACB=25°，

∵DE∥BC，

∴∠EDC=∠DCB=25°，∠BDE+∠B=180°，

∵∠B=70°，

∴∠BDE=110°，

∴∠BDC=∠BDE﹣∠EDC=110°﹣25°=85°．

∴∠EDC=25°，∠BDC=85°．

练习册系列答案
相关题目

【题目】②将多项式m2n－2mn＋n因式分解的结果是 ．

【题目】由于被墨水污染，一道几何题仅能见到如图所示的图形和文字：“如图，已知：四边形ABCD中，AD∥BC，∠D=67°，…”

（1）根据以上信息，你可以求出∠A、∠B、∠C中的哪个角？写出求解的过程；

（2）若要求出其它的角，请你添上一个适当的条件：　　　　　　，并写出解题过程．

【题目】小明与小华本学期都参加了5次数学考试(总分均为100分)，数学老师想判断这两位同学的数学成绩谁更稳定，在作统计分析时，老师需比较这两人5次数学成绩的(　　)

A. 平均数 B. 方差 C. 众数 D. 中位数

【题目】某商店老板将一件进价为800元的商品先提价50%，再打8折卖出，则卖出这件商品所获利润是元．

【题目】弹簧挂上物体后会伸长，已知一弹簧的长度（cm）与所挂物体的重量（kg）之间的关系如下表：

所挂物体的重量（kg）

0

1

2

3

4

5

6

7

弹簧的长度（cm）

12

12.5

13

13.5

14

14.5

15

15.5

（1）当所挂物体的重量为3kg时，弹簧的长度是_____________cm；

（2）如果所挂物体的重量为xkg，弹簧的长度为ycm，根据上表写出y与x的关系式；

（3）当所挂物体的重量为5.5kg时，请求出弹簧的长度。

（4）如果弹簧的最大伸长长度为20cm，则该弹簧最多能挂多重的物体?

【题目】如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是 ( ).

A. M点在线段AB上 B. M点在直线AB上

C. M点在直线AB外 D. M点可能在直线AB上,也可能在直线AB外

【题目】课外兴趣小组活动时，老师提出了如下问题：

（1）如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：

延长AD到E，使得DE=AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．

感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形或全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．

（2）问题解决：

受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．

①求证：BE+CF＞EF；②若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明；

（3）问题拓展：

如图3，在四边形ABDC中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作∠EDF为60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．

【题目】有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．

（1）列表或画树状图表示所有取牌的可能性；

（2）甲、乙两人做游戏，现有两种方案：A方案：若两次抽得相同花色则甲胜，否则乙胜；B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案获胜概率更高？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网