题目内容
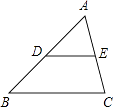
【题目】如图，在△ABC中，点D，E分别是边AB，AC的中点，设 
= 
， 
= 
． 
（1）求向量 
（用向量 ， 的式子表示）．
（2）在图中作出向量 
在向量 
， 方向上的分向量（不要求写作法，但要指出所作图中表示结论的向量）．
【答案】
（1）解：∵在△ABC中， 
= 
， 
= 
．
∴ 
= ﹣ = ﹣= ．
又∵E是边AC的中点，
∴ 
= 
．
故答案是：
（2）解：如图，
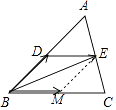
过点E作EM∥AB交BC于点M．
、 
即为向量 
在向量 
， 方向上的分向量
【解析】（1）首先利用平面向量三角形法则求得 ，然后由“E是边AC的中点”来求向量 ；（2）利用平行四边形法则，即可求得向量 ， 方向上的分向量．
练习册系列答案
中考解读考点精练系列答案
相关题目
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A.抛物线于x轴的一个交点坐标为（﹣2，0）
B.抛物线与y轴的交点坐标为（0，6）
C.抛物线的对称轴是直线x=0
D.抛物线在对称轴左侧部分是上升的
