Question

【题目】如图，在Rt△ABC中，∠B=90°，∠ACB=45°，∠D=30°，B、C、D在同一直线上，连接AD，若AB= ，则sin∠CAD= ．

Answer 1

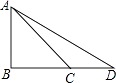
【答案】
【解析】解：∵在Rt△ABC中，∠B=90°，∠ACB=45°，
∴△ABC是等腰直角三角形，
∵AB= ，
∴BC=AB= ，AC= AB= ．
∵在Rt△ABD中，∠B=90°，∠D=30°，AB= ，
∴AD=2AB=2 ，BD= AB=3，
∴CD=BD﹣BC=3﹣ ．
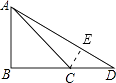
过C点作CE⊥AD于E．
∵S△ACD= ADCE= CDAB，
∴CE= = = ，
∴sin∠CAD= = = ．
所以答案是 ．

【考点精析】掌握解直角三角形是解答本题的根本，需要知道解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．