题目内容
【题目】如图，在平面直角坐标系中，AC⊥BC于点C，且点C在y的正半轴上，点A和点B分别在x的负半轴和正半轴，AC＝BC，AB＝8．
（1）求点C的坐标；
（2）点D从点C出发以1个单位/秒的速度向y的负半轴方向运动，同时点G从点B出发以1个单位/秒的速度向x轴的正方向运动，连接DG交直线BC于点F．设D、G两点运动时间为t秒，△DOF的面积为s，请用t的式子表示s，并直接写出t的取值范围；
（3）在（2）的条件下，过点F作FP⊥DF，过点C作x轴的平行线交FP于点P，连接AD，是否存在t，使△CPF的面积等于△AOD面积的2倍？如果存在，请求出t的值；如果不存在，请说明理由．
【答案】（1）C（0，4）；（2）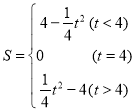
，（3）存在t，使△CPF的面积等于△AOD面积的2倍，t＝
或t＝
．
【解析】
（1）根据等腰直角三角形的性质可求得OC的长度，即可求出C点坐标；
（2）证明△DHF≌△GBF，根据全等三角形对应边相等可知点F是DG的中点，所以可证
,分情况讨论即可；
（3）先判断△POI为等腰直角三角形，利用面积公式表示出△CPF和△AOD的面积，用2倍建立方程，解出即可．
解：（1）∵AC＝BC，AB＝8，
∴OB＝4，
∵AC⊥BC，AC＝BC，
∴∠OBC＝45°．
∵∠BOC＝90°，
∴OC＝OB＝4，
∵点C在y的正半轴上，
∴C（0，4）；
（2）过点D作DH∥x轴交直线BC于点H，
∵DH∥x轴，∠BOC＝90°，∠OBC＝45°．
∴∠HDF＝∠BGF，∠CDH＝∠BOC=90°, ∠OCB＝45°,
∴CD=DH，
∵D，G两点速度相同，
∴CD＝DH＝BG，
在△DHF和△GBF中，
，
∴△DHF≌△GBF，
∴点F是DG的中点，
当0＜t＜4时，如图1，
∵OD＝4﹣t，OG＝4+t，
，
当t=4时，D点与O点重合，此时S=0，
如图2，当t＞4时，
∵OD＝t﹣4，OG＝4+t，
；
故 .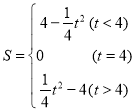
（3）如图3，
连接PD、PG、PO，过点F作E⊥CP于点E，过点P作PI⊥PO交x轴于点I，
∴△POI为等腰直角三角形，且OB＝BI＝OC＝CP，
∴点P（4，4），CP＝4．
当0≤t＜4时，EF＝
t+2，
S△CPF＝CP×EF＝×4×（t+2）＝t+4
S△AOD＝OA×OD＝×4×（4﹣t）＝8﹣2t
∴t+4＝2（8﹣2t），
解得t＝，
当t＞4时，EF＝t+2，
S△CPF＝CP×EF＝×4×（t+2）＝t+4
S△AOD＝OA×OD＝×4×（t﹣4）＝2t﹣8
∴t+4＝2（2t﹣8），
解得t＝．
∴存在t，使△CPF的面积等于△AOD面积的2倍，t＝或t＝．
