题目内容
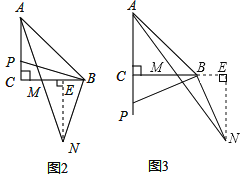
【题目】已知△ABC中,AC=BC,∠ACB=90゜,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90゜得线段BN,AN交直线BC于M.
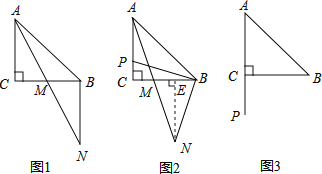
(1)如图1.若点P与点C重合,则![]() = ,
= ,![]() = (直接写出结果):
= (直接写出结果):
(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出![]() = .
= .
【答案】(1)1,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)先求出∠C=∠CBN,再利用“角角边”证明△ACM和△NBM全等,根据全等三角形对应边相等可得AM=MN,MC=MB,再求出AP=AC=2MC,然后求解即可;
(2)过点N作NE⊥BC于E,根据同角的余角相等求出∠PBC=∠BNE,然后利用“角角边”证明△PBC和△BNE全等,根据全等三角形对应边相等可得BE=PC,NE=BC,然后求出AP=CE,AC=NE,再利用“角角边”证明△ACM和△NEM全等根据全等三角形对应边相等可得MC=ME,整理即可得证;
(3)过点N作NE⊥BC交CB的延长线于E,然后与(2)的求解方法相同.
(1)解:∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠CBN=90°,BC=BN,
∴∠C=∠CBN,AC=BN,
在△ACM和△NBM中,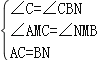 ,
,
∴△ACM≌△NBM(AAS),
∴AM=MN,MC=MB,
∴AP=AC=BC=MC+MB=2MC,
∴![]() =1,
=1,![]() =
=![]() ;
;
(2)证明:如图2,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,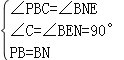 ,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC﹣PC=BC﹣BE=CE,AC=NE,
在△ACM和△NEM中,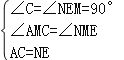 ,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∴CE=2MC,
∴AP=2MC;
(3)解:如图3,过点N作NE⊥BC交CB的延长线于E,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,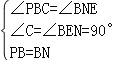 ,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC﹣PC=BC﹣BE=CE,AC=NE,
在△ACM和△NEM中,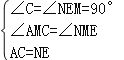 ,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∵AP=AC+PC,
CE=BC+BE=2MC,
∴AP=CE=2MC,
∴![]() =
=![]() .
.
故答案为:(1)1,![]() ;(3)
;(3)![]() .
.