题目内容
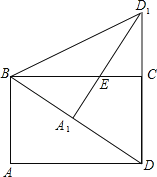
【题目】矩形ABCD中,∠DBA=60°,把△ABD绕点B逆时针旋转使得点A落在BD上,点A对称点为点A1,点D对称点为点D1,A1 D1与BC交于点E,连接D1C.

(1)求证:EC=EA1;
(2)求证:点D1、C、D在同一直线上.
【答案】见解析
【解析】
试题分析:(1)利用矩形的性质得∠ADB=∠DBC=30°,AD=BC,再根据旋转的性质得∠A1 BD1=∠ABD=60°,A1 D1=AD=BC,∠BD1 A1=∠ADB=30°,则∠D1B C=∠A1 BD1﹣∠DBC=30°,于是根据等腰三角形的判定得BE=ED1,所以EC=E A1;
(2)利用“SAS”可证明△B E A1≌△∠CED1,则∠D1CE=∠B A1 E=90°,所以∠D1CE+∠BCD=180°,于是可判断点D1、C、D在同一直线上.
(1)证明:∵矩形ABCD中,∠DBA=60°,
∴∠ADB=∠DBC=30°,AD=BC,
∵△BA1 D1是△ABD绕点B逆时针旋转所得,且点A落在BD上,
∴∠A1 BD1=∠ABD=60°,A1 D1=AD=BC,∠BD1 A1=∠ADB=30°,
∴∠D1B C=∠A1 BD1﹣∠DBC=60°﹣30°=30°,
∴∠D1B E=∠ED1B,
∴BE=ED1,
∴BC﹣BE=A1 D1﹣ED1,
∴EC=E A1;
(2)证明:在△B E A1和△∠CED1 中,
 ,
,
∴△B E A1≌△∠CED1,
∴∠D1CE=∠B A1 E=90°,
∴∠D1CE+∠BCD=90°+90°=180°,
∴点D1、C、D在同一直线上.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目