题目内容
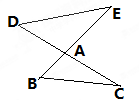
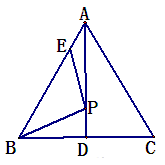
如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )。

A. | B. | C. | D. |
B.
试题分析:如图所示:
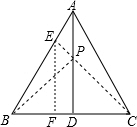
连接EC,交AD于点P,此时EP+BP最小,过点E作EF⊥BC于点F,
∵AD为等边△ABC边BC上的高,
∴B点与C点关于AD对称,
又∵AB=4,
∴BD=CD=2,
∴AD=2
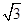 ,
,∵EF⊥BC,AD⊥BC,
∴EF∥AD,
∴△BEF∽△BAD,
∴
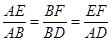 ,
,∴
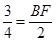 ,
,解得:BF=1.5,
∴FD=0.5,
∴EF=
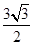 ,
,∴在Rt△EFC中
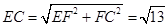 ,
,∴EP+BP的最小值为:EP+BP=
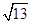 .
.故选B.
考点: 轴对称-最短路线问题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
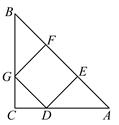
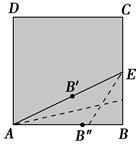
 =
= =
= =k,则k的值是
=k,则k的值是 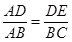 ,请添加一个条件,使
,请添加一个条件,使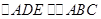 ,这个条件可以是______.
,这个条件可以是______.