题目内容
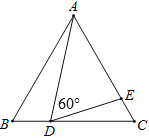
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．
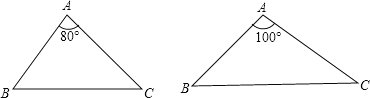
（1）请分别作出下图中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；
（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）．
【答案】(1)见解析;(2) 锐角三角形（和直角三角形）的最小覆盖圆是其外接圆；钝角三角形的最小覆盖圆是以其最长边为直径的圆
【解析】
第一个三角形是锐角三角形，那么它的最小覆盖圆应该是三角形ABC的外接圆；
第二个三角形是钝角三角形，那么它的最小覆盖圆应该是以BC为直径的圆．
解：（1）如图；
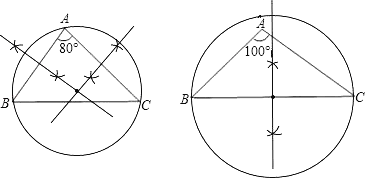
（2）锐角三角形（和直角三角形）的最小覆盖圆是其外接圆；钝角三角形的最小覆盖圆是以其最长边为直径的圆；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
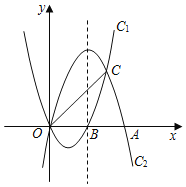
【题目】已知抛物线C：y＝x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C：y＝x2+2x﹣3 | A(_____) | B(_____) | (1，0) | (0，﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A，B两点的坐标，并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍，纵坐标变为原来的
，可证明得到的曲线仍是抛物线，(记为C1)，求抛物线C1对应的函数表达式.
