Question

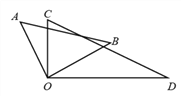
【题目】如图，将一副三角尺的直角顶点重合在一起.

（1）若 OB 是∠DOC 的角平分线，求∠AOD 的补角的度数是多少？

（2）若 ∠COB 与 ∠DOA 的比是 2:7，求 ∠BOC 的度数.

Answer 1

【答案】（1）45°（2）40°

【解析】试题分析：（1）根据角平分线的性质得出∠AOD的度数，即可得出结论；

（2）设∠COB=2x°，则∠DOA=7x°．由∠AOB=∠COD，可得∠AOC=∠DOB=2.5x°，则有2.5x°+2x°=90°，解出x的值即可得到结论．

试题解析：解：(1)∵OB 是∠DOC 的角平分线，∴∠COB=∠BOD=45°，∴∠AOD=90°+45°=135°，∴∠AOD的补角=180°-135°=45°；

（2）设∠COB=2x°，则∠DOA=7x°．

∵∠AOB=∠COD，∴∠AOC=∠DOB=(7x°-2x°)÷2=2.5x°，∴2.5x°+2x°=90°，解得：x=20．

∴∠BOC=2x°=40°．