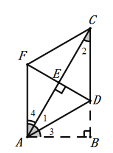
题目内容
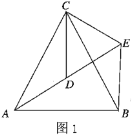
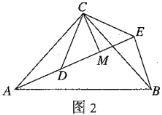
【题目】如图,在![]() 中,
中,![]() .将
.将![]() 向上翻折,使点
向上翻折,使点![]() 落在
落在![]() 上,记为点
上,记为点![]() ,折痕为
,折痕为![]() ,再将
,再将![]() 以
以![]() 为对称轴翻折至
为对称轴翻折至![]() ,连接
,连接![]() .
.
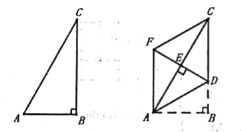
(1)证明:![]()
(2)猜想四边形![]() 的形状并证明.
的形状并证明.
【答案】(1)见解析;(2)四边形ADCF为菱形,证明见解析.
【解析】
(1)根据翻折的性质,先得出AB=AE,∠AED=90°,再根据AC=2AB,可得出DE垂直平分AC,从而可得出结论;
(2)根据折叠的性质以及等边对等角,先求出∠1=∠2=∠3=∠4=30°,从而可得出∠FAB=90°,进而推出AF∥CD,再由边的等量关系,可证明四边形ADCF为菱形.
(1)证明:由轴对称得性质得,
∠B=90°=∠AED,AE=AB,
∵AC =2AB,
∴ED为AC的垂直平分线,
∴AD=CD;
(2)解:四边形ADCF为菱形.证明如下:
∵AD=CD,∴∠1=∠2.
由轴对称性得,
∠1=∠3,∠1=∠4.
∵∠B=90°,
∴∠1=∠2=∠3=∠4=30°,
∴∠FAB=90°,
∴AF∥CD,AF=AD=CD,
∴四边形ADCF为菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目