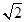题目内容
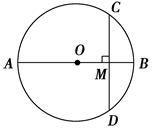
如图，在△ABC中，AB＝AC，以AB为直径的⊙O交AC于点E，交BC于点D，连接BE、AD交于点P.求证：
(1)D是BC的中点；
(2)△BEC∽△ADC.
(1)D是BC的中点；
(2)△BEC∽△ADC.
（1）（2）见解析
证明：(1)∵AB是⊙O的直径，
∴∠ADB＝90°，即AD⊥BC，
∵AB＝AC，∴D是BC的中点；
(2)∵AB是⊙O的直径，∴∠AEB＝∠ADB＝90°，
即∠CEB＝∠CDA＝90°，
∵∠C是公共角，∴△BEC∽△ADC.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
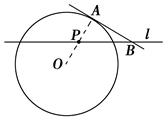
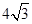cm，P为直线l上一动点，以1cm为半径的⊙P与⊙O没有公共点．设PO=dcm，则d的范围是 ．
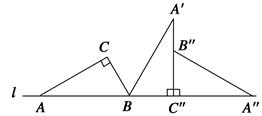
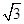，则顶点A运动到点A″的位置时．
