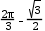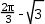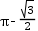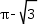题目内容
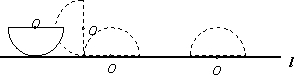
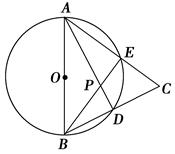
如图,⊙O的半径为4cm,直线l与⊙O相交于A、B两点,AB=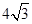 cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .
cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .

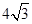 cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .
cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .
d>5或2≤d<3.
此题主要考查了圆与圆的位置关系,根据图形进行分类讨论得出是解题关键.根据两圆内切和外切时,求出两圆圆心距,进而得出d的取值范围.
解:连接OP、OA,
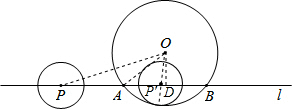
∵⊙O的半径为4cm,⊙P的半径为1cm,⊙P与⊙O没有公共点,
∴d>5时,两圆外离,
当两圆内切时,过点O作OD⊥AB于点D,
OP′=4﹣1=3cm,OD=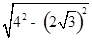 =2(cm),
=2(cm),
∴以1cm为半径的⊙P与⊙O没有公共点时,2≤d<3,
故答案为:d>5或2≤d<3.
解:连接OP、OA,
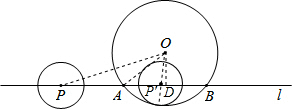
∵⊙O的半径为4cm,⊙P的半径为1cm,⊙P与⊙O没有公共点,
∴d>5时,两圆外离,
当两圆内切时,过点O作OD⊥AB于点D,
OP′=4﹣1=3cm,OD=
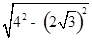 =2(cm),
=2(cm),∴以1cm为半径的⊙P与⊙O没有公共点时,2≤d<3,
故答案为:d>5或2≤d<3.

练习册系列答案
相关题目
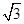 为半径作圆,点M(a,b) 是⊙P上的一点,设
为半径作圆,点M(a,b) 是⊙P上的一点,设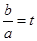 ,则
,则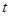 的取值范围是 .
的取值范围是 . 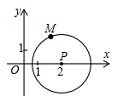
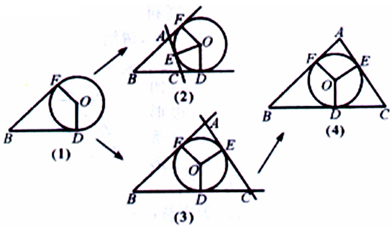

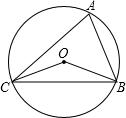
 的⊙O是△ABC的外接圆,∠CAB=60°,则BC= .
的⊙O是△ABC的外接圆,∠CAB=60°,则BC= .