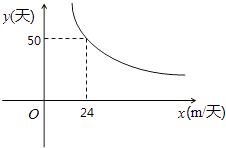
题目内容
【题目】如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为 
的中点． 
（1）求证：AB=BC；
（2）求证：四边形BOCD是菱形．
【答案】
（1）证明：∵AB是⊙O的切线，
∴OB⊥AB，
∵∠A=30°，
∴∠AOB=60°，
∵OB=OC，
∴∠OCB=∠OBC= 
∠AOB=30°，
∴∠A=∠OCB，
∴AB=BC
（2）证明：连接OD，
∵∠AOB=60°，
∴∠BOC=120°，
∵D为 
的中点，
∴ 
= 
，∠BOD=∠COD=60°，
∵OB=OD=OC，
∴△BOD与△COD是等边三角形，
∴OB=BD=OC=CD，
∴四边形BOCD是菱形．
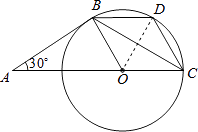
【解析】（1）由AB是⊙O的切线，∠A=30°，易求得∠OCB的度数，继而可得∠A=∠OCB=30°，又由等角对等边，证得AB=BC；（2）首先连接OD，易证得△BOD与△COD是等边三角形，可得OB=BD=OC=CD，即可证得四边形BOCD是菱形．
练习册系列答案
名校课堂系列答案
相关题目
【题目】甲、乙两名队员参加射击训练，成绩分别绘制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
（1）写出表格中a，b，c的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击成绩，若选派其中一名参赛，你认为应选哪名队员？
【题目】如图是一个在平面直角坐标系中从原点开始的回形图，其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格：
点 | 坐标 | 所在象限或坐标轴 |
A | ||
B | ||
C | ||
D | ||
E | ||
F |
(2)在图上将回形图继续画下去(至少再画出4个拐点)；
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系；
