题目内容
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A. D. C三点重合),过点P作PQ⊥AB,垂足为Q,交直线BD于E.

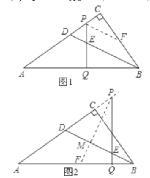
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)作∠CPQ的角平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由。
【答案】(1)见解析;(2)PF∥BD;理由详见解析;PF⊥BD,理由见解析;
【解析】
(1)由PQ与AB垂直,得到一对直角相等,理由直角三角形的两锐角互余得到两对角互余,再BD为角平分线,利用角平分线定义得到一对角相等,再由对顶角相等,利用等量代换即可得证;
(2)分两种情况,当P在线段AC上时,如图1所示,可得出PF与BD平行,由第一问的结论利用等角对等边得到PD=PE,利用角平分线定义及外角性质得到一对内错角相等,利用内错角相等两直线平行即可得证;当P在AC延长线时,PF垂直于BD,由PD=PE,利用三线合一即可得证.
(1)∵PQ⊥AB,
∴∠EQB=∠C=90°,
∴∠BEQ+∠EBQ=90°,∠CBD+∠PDE=90°,
∵BD为∠ABC的平分线,
∴∠CBD=∠EBQ,
∵∠PED=∠BEQ,
∴∠PDE=∠PED;
(2)当P在线段AC上时,如图1所示,此时PF∥BD,
理由为:∵∠PDE=∠PED,
∴PD=PE,
∵PF为∠CPQ的平分线,∠CPQ为△PDE的外角,
∴∠CPF=∠QPF=∠PDE=∠PED,
∴PF∥BD;
当P在线段AC延长线上时,如图2所示,PF⊥BD,
理由为:∵∠PDE=∠PED,
∴PD=PE,
∵PM为∠CPQ的平分线,
∴PF⊥BD.

【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
图书类别 | 画记 | 人数 | 百分比 | ||
文学类 | |||||
艺体类 | 正 | 5 | |||
科普类 | |||||
其他 | 正正 | 14 | |||
合计 | a | 100% |
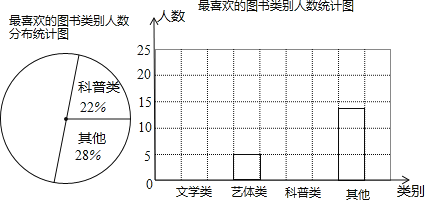
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量![]() 为________;
为________;
(2)在扇形统计图中,“艺体类”所在的扇形圆心角应等于_________度;
(3)补全条形统计图;
(4)已知该校有![]() 名学生,估计全校最喜欢文学类图书的学生有________人.
名学生,估计全校最喜欢文学类图书的学生有________人.
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0




